2024/6/30 upd:填坑。

2025/5/26 upd:添加势能线段树方面内容。

数据结构总结

最喜欢的一集。

本文md源码长度 80K/2200行，请只用 Ctrl+F 查询您想看的部分

OI 中所指的数据结构是一种用于存放数据的结构，一般而言高效的数据结构可以以高效率完成一系列给定的操作。

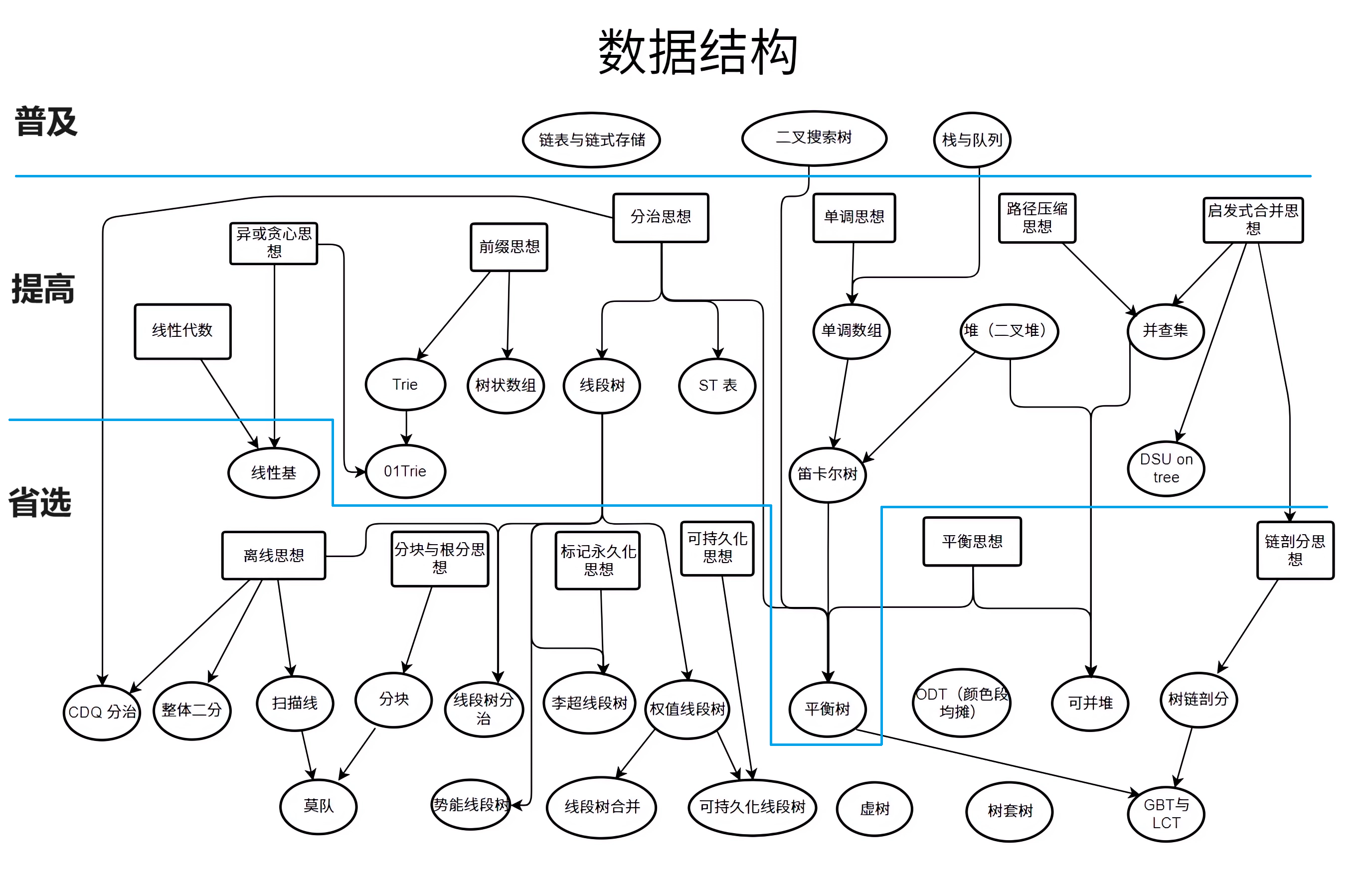
先放张图震楼：

（其实这张图里少了个可持久化 Trie，因为实在是塞不下了）

~~不要问为啥没有 K-d Tree，因为 lxl 讲的时候声称不要写（~~

本文不只是数据结构哦。

在阅读本文前，请确保已经掌握了以下内容：

链表与链式结构
栈与队列
树的基本定义与遍历

为防止本文长度过长，将仅给出部分模板代码。

若无特殊说明，。

基础

二叉堆

操作

维护一个集合，支持以下操作：

插入一个值或删除最值
询问最值

思想

堆是一棵完全二叉树，满足都有的父亲是。

堆的性质：父亲结点的权值比两儿子小/大。我们称父亲结点的权值比儿子小的为小根堆，反之为大根堆。下文只讨论小根堆。

容易发现，根结点就是最小值。

插入时我们将元素先放到的位置，然后不断地与其父亲交换直到其父亲不大于其本身。（向上调整）

删除时我们将与位置的数交换，然后不断地将其与较小的儿子交换直到它比两儿子都小。（向下调整）

时间复杂度分析

插入与删除操作的时间复杂度都取决于树高，而树高为，因此时间复杂度。

拓展

如果我们要一次性将个元素建为一个堆，我们可以使用一种时间复杂度的算法而非一个一个插入。

我们随意地将值填入，然后对于所有非叶结点执行向下调整操作。

时间复杂度证明（贺自 OI-Wiki）：从结点开始向下调整是的，因此总时间复杂度

由于实际应用中几乎不可能需要手写堆，因此不给出模板。

STL

`std::priority_queue`

包含在 queue 头文件。

功能：堆。

定义一个 int 类型的大根堆：

1	std::priority_queue<int> pq;

定义一个 int 类型的小根堆（须包含 functional 头文件）：

1	std::priority_queue<int,std::vector<int>,std::greater<int>> pq;

取出堆的最值：

1	int p=pq.top();

删除堆的最值：

pq.pop();

插入一个值：

1	pq.push(x);

完整演示：

#include<bits/stdc++.h>

int main(){
    std::priority_queue<int> pq;
    pq.push(1),pq.push(2);
    printf("%d\n",pq.top());
    pq.pop();
    pq.push(4),pq.push(3);
    printf("%d\n",pq.top());
    printf("%d\n",pq.size());
    while(!pq.empty())printf("%d ",pq.top()),pq.pop();
    return 0;
}
/*
output:
2
4
3 1 
*/

`std::make_heap`

make_heap、pop_heap、push_heap 是三个关于堆的函数，其作用分别为将数组建为堆、删除最值、插入一个值。

但是一般也不用。

对顶堆

你需要维护一个集合，支持操作：

插入元素。

查询中位数。输出中位数的平均数。

。

设当前集合大小为。

我们可以考虑维护两个堆，一个大根堆维护前小的元素，一个小根堆维护其余的元素，此时我们发现中位数就是小根堆的堆顶（奇数）或两个堆堆顶的和（偶数）。

对于插入操作，我们判断插入的数与小根堆大小的关系并插入对应的堆。

在插入操作后若小根堆大小不再是或大根堆大小不再是我们就需要取出大小太大的堆里的元素放到大小太小的堆里。

时间复杂度。

并查集

操作

维护若干个集合，支持用或的时间复杂度执行以下操作：

合并两元素所在的集合。
查询两个元素是否在同一集合中。

思想

我们考虑记录一个点究竟在哪个集合中。

为了方便，我们用一个集合的代表元素来代表整个集合。在初始时，每个集合的代表元素都是其本身。

那么如果两个元素所在集合代表元素相同，那么两个元素在同一集合中；反之则不在。

而如果我们要合并两元素所在的集合，直接找到两元素所在集合的代表元素，更改其中一个的代表元素为另一个即可。

实现

我们用树来实现。

我们每个元素记录一个，表示其代表元素就是的代表元素。如果，说明的代表元素就是其本身。初始时所有。

查询代表元素只需不断跳即可。

1	int find(int x){return fa[x]==x?x:find(fa[x]);}

优化

ちょっと待って，我可以把这棵树构造成一条链这样就卡成的啊不是说好了是嘛？

别急，这有个两个优化。

路径压缩

我们只需稍稍修改上面提到的 find 函数：

1	int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}

这段代码的意思：如果一个元素的代表元素是它本身，那么返回它本身；否则查询其代表元素的代表元素，并把本身的代表元素改为查询结果。

举个例子，如果我们通过某种邪恶的方式构造了这样的图：

那么在执行 find(1) 后图就会变成

感性理解这样可以显著降低复杂度，因为大大减小了树高。

这里不加证明地给出路径压缩的均摊复杂度是的。

启发式合并/按秩合并

我们对于代表元素额外记录其集合的大小或深度。

在合并时，我们总是将大小或深度较小的集合合并到较大的一个。

这样保证了树高是的（要使树高变为需要个结点），因此时间复杂度。

我们将按集合大小合并的叫做启发式合并，按树高合并的叫做按秩合并。

同时使用上述两个优化的均摊时间复杂度非常近似于均摊（实际上是，是 Ackermann 函数的反函数，一般取）。

模板

struct UFS{
    private:
        vi fa,siz;
        int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
    public:
        UFS(int n=0){
            fa.resize(n+1),siz.resize(n+1,1);
            for(int i=1;i<=n;++i)fa[i]=i;
        }
        bool mrg(int u,int v){//成功合并返回1，失败合并返回0
            u=find(u),v=find(v);
            if(u==v)return 0;
            if(siz[u]>siz[v])std::swap(u,v);
            fa[u]=v;siz[v]+=siz[u];
            return 1;
        }
        bool family(int u,int v){return find(u)==find(v);}
};

带撤销的并查集

你需要维护一系列集合，支持以下操作：

合并两个集合。

查询两个元素是否在同一个集合中。

查询一个集合的大小。

撤销上一次合并操作。

。

我们可以开一个栈，记录每一次合并的两个元素、原来的父亲、原来的大小，在合并时往这个栈里压进去就好，撤销时取出栈顶将操作还原即可。

注意这里不能用路径压缩，因为路径压缩会改一车父亲。

时间复杂度。

带权并查集

SPOJ CORNET - Corporative Network

题意：你需要维护一系列树，边有边权。

操作 1：在两个点之间连一条边。

操作 2：询问一个点到根的边权和。

保证任意时刻图是一棵树。

我们考虑用并查集维护，同时记录每个结点到根的权值和。

在 find 操作时，我们发现只需要记录到父亲的边权，然后在路径压缩时再计算父亲到根的距离即可。

注意这道题不能用启发式合并，因为合并的方向已经指定。

单调数组

操作

Luogu1886 滑动窗口/Luogu5788 单调栈

单调数组分为单调队列和单调栈。

单调队列一般用于解决在某个区间内的最值。如果这个区间长度是固定的（如滑动窗口）可以做到的时间复杂度，否则可能需要结合二分做到的时间复杂度。

单调栈一般用于解决“某个元素在数组中左边/右边第一个比它大的元素”，时间复杂度。单调栈与笛卡尔树有着密切的关系。

单调数组大部分时候并不会作为一个单独的数据结构出现，而是往往和 DP 狼狈为奸恶心考生。

思想

单调数组中会有若干个数，满足其序号单调递增且值单调。我们下文假定值单调递减。

我们从开始升序放入元素。当我们放入时为了维持值单调递减就会把所有的弹出。这样我们就发现了对于这些被弹出的就有是它们右边第一个比更小的元素（否则应该在更早的时候就被弹出了）。

对于滑动窗口问题，我们可以发现单调栈中栈底的元素就是的最大值。为了能求，我们需要每次都把已经不在这个区间里的数从栈底弹出。然后我们发现这已经不是一个栈了，而是队列了。

（所以其实单调队列不是队列而是双向队列）

时间复杂度分析

每个元素只会被进栈/出栈（或队列）一次，因此时间复杂度均摊。

但是这个是均摊的，因此单调数组很难撤销。

二叉搜索树

操作

维护一个集合，支持进行以下操作：

插入一个数。
删除一个数。
查询一个数在集合内的排名。
查询集合内第小的数。
查询一个数在集合内的前驱（最大的比它小的数）与后继（最小的比它大的数）。

思想

二叉搜索树（Binary Search Tree,BST）是一棵二叉树，满足对于任意结点：

如果它有左儿子，那么它左儿子的点权小于它自己。
如果它有右儿子，那么它右儿子的点权大于它自己。

容易发现二叉搜索树的中序遍历中点权是递增的。

插入

我们从根结点开始。

如果当前结点是空，插入到这里即可。
如果待插入值小于这个结点的值，说明这个数应当插在左子树内。转移到左子。
否则说明这个数应当插在右子树内。转移到右子。

查询第 k 小

我们在每个结点都记录其子树大小。

我们还是从根结点开始。设当前结点左子树大小为，说明当前结点是第小。那么：

如果，已经找到了。
如果，说明在左子树，转移到左子。
如果，说明在右子树，转移到右子并将减小到。

其他的查询操作和 k 小非常类似不再赘述。

删除

我们先找到这个结点的位置，然后大力分讨：

如果这个结点的儿子数不大于，那么直接把它的（可能存在的）子树接到它的父亲上就好。
否则我们在子树内找到它的后继，然后把这个结点提上去顶替待删除元素的位置。

但是由于实在是太麻烦了等一系列原因我们根本不会在此实现删除。

事实上普通 BST 就是个垃圾谁写我笑他两年半因为就连 std::vector 和 std::lower_bound 都比它更优。

时间复杂度分析

操作次数取决于树高，树高最坏是的，因此单次操作时间复杂度。

甚至不如 std::vector+std::lower_bound。

另：期望树高实际上是的但是没有睿智出题人会出随机数据。

所以在实际实现中是不可能写普通 BST 的。

进阶

树状数组

操作

维护一个数组，支持的时间复杂度进行以下操作：

单点修改
查询前缀

如果维护的信息具有结合律与可减性（如前缀和、模质数意义下的前缀积等），可以用差分思想做成区间查询。

思想

我们定义一个数的为其二进制下最低为的位单独取出的值。如则，则。

这样我们就可以把一个数拆成若干的次幂相加，方法是不断减掉这个数的。

树状数组（Binary Indexed Tree，BIT，也称 Fenwick Tree）的核心思想就在于把一段前缀拆成个区间然后维护这些区间的信息。我们规定结点维护的区间信息，如下：

这样的好处在于可以通过不断减去从而快速将一个前缀和拆成若干的区间和。

我们将一个数写成二进制，以为例：

在减去后会依次变成。

而我们要查询位置的前缀，我们就会分别取出、、这三段区间，将其合并恰好是。

现在我们尝试证明：无论取什么数，按照这个规则取出的区间合并起来都一定是其前缀。

我们设在二进制下从低到高的第为，那么我们通过减得到的数分别为

我们为了方便把这个数列命名为，那么。

那么我们考察数列中相邻的两项，那么这两项管辖的区间分别是与。

而，因此这两个区间的并集恰好没有“留缝”。

而管辖的区间一定是，因此每一段区间都能拼起来“不留缝”，因此这样就可以查询出其前缀和。

我们现在考虑如何修改。

显然，我们只需要修改包含待修改位置的区间的值。我们现在考虑如何快速找出所有包含它的区间。

这里的结论比上一节更加逆天：我们只需要不断地加上就可以遍历所有包含它的区间。

证明过于繁琐就不放了。

感性理解：在把末尾的一串改为后是会包含这个结点的。

最后我们还有一个问题：如何快速求。

这里有一个非常简洁的写法：。

proof：

C艹中存储负数用补码，也就是把二进制位都取反再。

我们设 $个$ ，显然。

我们考虑它每一位都取反后就变成了 $个$ ，再加一就会变成 $个$ 。

由于取反后是，那么这部分取反后是；而后面那部分又恰好是全反的，只有第位在两个数里都是，我们就求得了 lowbit。

实现

BIT 可能是最短的序列维护数据结构了，其核心代码就两行（以前缀和为例）：

1 2	void add(int x,int k){for(;x<=n;x+=x&(-x))T[x]+=k;} int prefix(int x){int ans=0;for(;x;x-=x&(-x))ans+=T[x];return ans;}

模板

struct BIT{
    private:
        vector<int> T;
        int n;
    public:
        BIT(int _n){T.resize((n=_n)+1);}
        void add(int x,int k){for(;x<=n;x+=x&(-x))T[x]+=k;}
        int prefix(int x){int ans=0;for(;x;x-=x&(-x))ans+=T[x];return ans;}
};

时间复杂度分析

无论是加还是减都会最多跳次，因此时间复杂度。

此外 BIT 的常数也极为优秀。

二维树状数组

如果我们要进行二维的操作，那么我们可以把 BIT 的结点也变成 BIT，这样就得到了二维 BIT。

修改和查询也只需要多一维即可。时间复杂度。

拓展：BIT 上二分

Luogu6619 [联合省选2020]冰火战士

转化后题意：你需要维护两个集合，支持以下操作：

向一个集合中插入一个元素，元素的编号为，权值为。

撤销某次插入操作。

每次操作后查询，使中不大于的元素权值和与中不小于元素权值和中的较小值最大。输出和这个值的两倍。

，3s

我们发现中不大于的元素权值和随着增大而增大，中不小于元素权值和随着增大而减小，画到同一个平面直角坐标系里会在某个地方相交，而相交点就是我们要求的最大值。

自然的想法自然是用 BIT 维护前缀/后缀和然后二分最大的前缀小于后缀的位置然后取这一个和下一个位置中较大的一个为答案，但是单次二分是的，总时间复杂度，无法承受。

此时我们考虑 BIT 天然就是一个倍增的结构，能否就在这个 BIT 上二分呢？

答案是肯定的。我们考虑我们在查询时拆出了个区间，而这个个区间的长度都是的整数次幂的，因此我们可以直接在这棵 BIT 上二分。

具体的，我们令从开始递减枚举（），初始在位置，每次尝试向后跳步（即到达），如果跳过这一步前缀和已经大于后缀和说明跳多了，这一步就不跳；否则就跳。我们发现由于我们是从高到低倍增则不增，因此每一次跳步其实就是在答案上加（根据管辖区间即可证明），这样时间复杂度就降为。

最终时间复杂度。

线段树

操作

维护一个序列，支持的区间修改、区间查询。

线段树的维护物须满足结合律、分配律并且可以用分治高效解决（即快速合并）。

BIT 能做的线段树都能做。

思想

线段树（Segment Tree）是一棵完美二叉树（即非叶结点都有两个儿子），每一个结点管辖一个区间。设某结点管辖的区间是，那么其左右儿子管辖的区间分别是和，其中。根结点管辖的区间是。

对于每个结点，它的信息是由它的两个儿子合并而来的。这一操作被称为上传（pushup）。

单点修改

我们先从简单的情形开始。

我们设要修改位置的值。

我们从根结点开始。

若，此时，直接修改即可。结束递归。
若，说明待修改的值在左子树，递归到左子树。
否则说明待修改的值在右子树，递归到右子树。
在访问完一个结点后，其儿子的信息可能改变，因此重新 pushup。

区间查询

我们设要查询区间的信息。

我们还是从根结点开始。

若，说明当前结点被询问区间完全包含，直接返回即可。
若，说明询问区间有一部分在左子树中，需要递归到左子树返回并合并答案。
若，说明询问区间有一部分在右子树中，需要递归到右子树返回并合并答案。
返回当前合并的答案即可。

区间修改

当需要区间修改时我们不可能直接把所有影响到的结点都改了，此时我们需要引入懒标记（lazy tag）思想。

以区间加为例：我们考虑对线段树上的一个结点执行区间加的影响就是这个区间的和加上或区间的最大值加上。

此时我们在对结点进行了这样的操作后，在这个结点上打上标记，表示在这个区间上曾经执行了一个关于的操作。

我们在递归到一个结点执行操作或查询时，如果这个结点上有标记，我们将这个结点上的标记下方到两个儿子上并同时对这两个儿子进行影响，这样访问儿子时才能获得正确的信息。这个操作被称为标记下传（pushdown）。

这样我们就可以执行区间修改了。

我们还是从根结点开始。

若，说明当前结点被修改区间完全包含，直接修改并返回即可。
下放懒标记。
若，说明修改区间有一部分在左子树中，需要递归到左子树修改。
若，说明修改区间有一部分在右子树中，需要递归到右子树修改。
执行 pushup。

同理，我们也需要在区间查询时在判断是否为完全包含区间后下放懒标记再递归子树。

懒标记是很多线段树的重要一环，懒标记设计的好坏可能直接影响正确性与效率。

建树

我们可以进行建树。

从根结点开始。

若，执行单点修改即可。
递归到左右子树。
执行 pushup。

时间复杂度分析

我们设合并信息的时间复杂度为。

对于区间操作，可以证明我们访问区间的个数是的。

proof：在一层内不可能同时访问超过个结点（访问的结点管辖的区间是连续的，如果超过个则一定会存在两个结点，它们的父亲就已经结束向下递归），而最多层。

因此时间复杂度。在大多数情况下。

实现

在实现中我们一般使用堆式线段树，即结点的左右儿子分别为与。

注意这种线段树的空间要开四倍。

模板

struct node{
    //在这里定义你的维护物
};
struct tag{
    //在这里定义你的懒标记
};
node mrg(node x,node y){
    //在这里定义你的合并方式
}
struct sgt{
    #define ls (p<<1)
    #define rs ((p<<1)|1)
    #define mid ((s+t)>>1)
    private:
        vector<node> T;
        vector<tag> Tag;
        int n;
        void pu(int p){T[p]=mrg(T[ls],T[rs]);}//上传
        void adt(int p,int s,int t,tag x){
            //在这里定义你的标记下传方式
        }
        void pd(int p){
            if(/*有标记*/){
                adt(ls,s,mid,Tag[p]),adt(rs,mid+1,t,Tag[p]);
                tag[p]=/*无标记*/;
            }
        }
    public:
        sgt(int _n=0,vi a={}){
            int siz=(n=_n)*4+50;
            T.resize(siz);Tag.resize(siz);
            std::function<void(int,int,int)> bu=[&](int p,int s,int t){
                if(s==t)return /*单点修改*/,void();
                bu(ls,s,mid),bu(rs,mid+1,t),pu(p);
            };bu(1,1,n);
        }
        node qry(int l,int r){
            std::function<node(int,int,int)> qr=[&](int p,int s,int t){
                if(l<=s&&t<=r)return T[p];
                pd(p,s,t);
                if(l<=mid){
                    if(r>mid)return mrg(qr(ls,s,mid),qr(rs,mid+1,t));
                    return qr(ls,s,mid);
                }
                else return qr(rs,mid+1,t);
            };
            /*
            当维护的信息计算空集比较方便时：
            std::function<node(int,int,int)> qr=[&](int p,int s,int t){
                if(l>t||s>r)return 空集;
                if(l<=s&&t<=r)return T[p];
                return pd(p,s,t),mrg(qr(ls,s,mid),qr(rs,mid+1,t));
            };
            */
            return qr(1,1,n);
        }
        void mdf(int l,int r,/*修改信息*/){
            std::function<void(int,int,int)> md=[&](int p,int s,int t){
                if(l>t||s>r)return;
                if(l<=s&&t<=r)return adt(p,s,t,/*修改信息*/);
                pd(p,s,t),md(ls,s,mid),md(rs,mid+1,t),pu(p);
            };
            md(1,1,n);
        }
    #undef ls
    #undef rs
    #undef mid
};

由于线段树的拓展太多，此处仅稍作拓展，剩下的部分放到拔高篇。

动态开点线段树

线段树也可以做到动态开点，即用链式结构存储。

当我们访问一个结点时，如果这个结点为空，我们才把这个结点建出来。

这样的好处是节省空间，坏处是会稍稍提高常数。

权值线段树

线段树可以维护序列，同时也可以维护值域，相当于在桶上开了棵线段树，每个结点管辖的区间是一个值域。

在值域很大的时候，我们不得不采取动态开点。

分析空间复杂度：线段树有层，每插入一个数就要开个结点，因此需要的空间。

我们可以用的时间复杂度用权值线段树干很多事，包括但不限于什么查 kth、rank、前驱、后继之类，光凭这一点就薄纱 BST 了。不过会被卡空间。

字典树（Trie 树）

操作

维护一系列字符串，支持：

插入一个字符串（为字符串长度）。
查询一个字符串的出现次数。

思想

Trie 树是一棵叉树，其中是字符集大小。

Trie 的思想在于每一个结点都代表一个字符串，每一条边都是“转移”，表示走这条边后要在父亲结点代表的字符串，字符串的值是根到这个结点上所有边的权值顺次拼接。

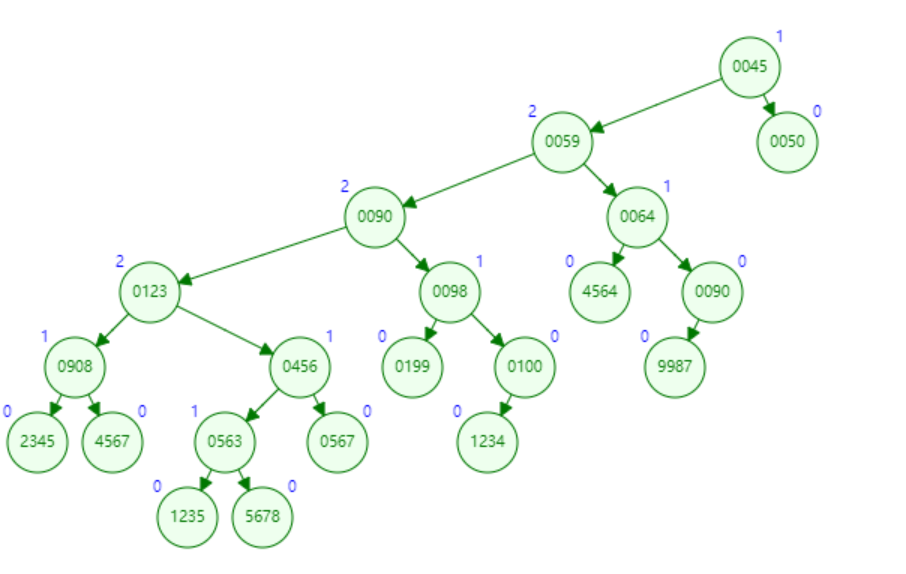
下图即为的 Trie 树。

插入

我们令。

我们遍历字符串的每个字符：

如果没有这个转移，我们新建这一个结点。
。

在结尾结点打结束标记。

查询

我们令。

我们遍历字符串的每个字符：

如果没有这个转移，返回不存在。
。

返回结尾处有没有结束标记。

模板

const int SIGMA=26;//字符集大小
struct Trie{
    typedef std::array<int,SIGMA> node;
    private:
        vector<node> T;
        vector<int> end;//以每个结点为结尾的字符串个数
           int nt;
        int get(char x){return x-'a';}
    public:
        Trie(){T.resize(1),end.resize(1),nt=0;}
        void ins(std::string s){
            int pos=0;
            for(auto v:s){
                int &p=T[pos][get(v)];
                if(!p)p=++nt,T.push_back(node()),end.push_back(0);
                pos=p;
            }
            end[pos]++;
        }
        int qry(std::string s){
            int pos=0;
            int pos=0;
            for(auto v:s){
                int &p=T[pos][get(v)];
                if(!p)return 0;
                pos=p;
            }
            return end[pos];
        }
};

Trie 树在字符串中的更多应用参见字符串一文。

01Trie

如果我们把数也写成二进制并从高位到低位排列，那么每个数也可以理解为一个字符串。这样我们就可以把数也插入到 Trie 树中，这样的 Trie 被称为 01Trie。

01Trie 可以用来解决的问题包括：

集合中选择两个数使异或和最大。
作为一种特殊的权值线段树使用。

ST 表

操作

维护一个序列，支持预处理与静态区间最值查询。

思想

ST 表（Sparse Table，稀疏表）是一种基于倍增的数据结构，用于解决静态 RMQ 问题。

我们可以先考虑一个 DP：表示到区间内的最大值，则

很好理解。

ST 表就是基于这个 DP 处理出所有位置往后跳步区间内的最大值，在查询区间时我们就只需要查询与的较大值即可。

但是这个是啥啊？

我们为了不漏掉区间内的任何一个数，需要，则，解得；而我们也不能包含查询区间外的数，需要，解得。

综上，。

模板


#define lg std::__lg // 2024/02/21 upd：根据著名队爷 platelet 的实验，std::__lg 吊打预处理

struct st{
    const int MAXN=21;
    private:
        int n;
        vector<vector<int>> st;
    public:
        stt(int _n=0,vector<int> a={}){
            st.resize(MAXN,vector<int>((n=_n)+1));
            st[0]=a;
            for(int j=1;j<MAXN;++j)
                for(int i=1;i+(1<<j)-1<=n;++i)
                    st[j][i]=std::max(st[j-1][i],st[j-1][i+(1<<(j-1))]);
        }
        int qry(int l,int r){
            int k=lg(r-l+1);
            return std::max(st[k][l],st[k][r-(1<<k)+1]);
        }
};

笛卡尔树

操作

维护一个序列，支持预处理与或静态区间最值查询。

思想

笛卡尔树同时是一个堆和一棵二叉搜索树。

具体的，树上每个结点有两个权值。按照看，笛卡尔树是一棵二叉搜索树；按照看，笛卡尔树是一个堆。

在解决 RMQ 问题时，我们将数组的下标看作，把值看作，然后构建笛卡尔树。

笛卡尔树的性质：若分别互不相同，则笛卡尔树唯一。

构造过程

下文以区间最大值为例。此时堆是大根堆。

可以用单调栈在时间内求出笛卡尔树。

我们将升序排列（在这个场景下并不需要，因为数组下标天然升序），然后顺次插入。

为了维持二叉搜索树的性质，新插入的结点必须在目前树的最右链末端（即一直向右子树走得到的链，因为我们需要保证在中序遍历意义下是最后一个点）；但是为了维护堆的性质，我们需要找到最右链第一个比它大的位置，然后让它成为为的右儿子，再把原来的右儿子接到的左儿子上（维护二叉搜索树性质）。

我们发现最右链的维护过程非常类似单调栈，因此可以设计下列算法：

初始时单调栈为空。

对于：

将单调栈中小于的值全部弹出。
将此时单调栈顶的元素的右儿子设置为。
将的左儿子设置为最后一个被弹出的元素。
将入栈。

时间复杂度。

询问

。

证明：到路径上的链取出来后，链“下方”（包含本身）的区间就是的区间。根据堆的性质得证。

因此我们可以用 RMQ 求 LCA 的方法做到预处理+ 查询。（猜您想找：CSP-S 2021 初赛）

不过这个方法常数巨大，在此不作详细介绍；更好的方法其实是树剖做到常数很小的询问或者普通 ST 表的的预处理（不过这样就都去写 ST 表了吧？）

模板

vi a(n+1);for(int i=1;i<=n;++i)a[i]=read();
vi sta(n+1),ls(n+1),rs(n+1);
int top=0;
for(int i=1;i<=n;++i){
    int lst=0;
    while(top&&a[sta[top]]<a[i])lst=sta[top--];
    if(top)rs[sta[top]]=i;
    ls[i]=lst;
    sta[++top]=i;
}

平衡树

操作

与二叉搜索树相同。不同点在于将这些操作时间复杂度都降到了。

此外还可以用来维护序列，支持序列的翻转、移动、插入等，时间复杂度均为。

可以做线段树能做的所有事情。

思想

平衡

平衡树实际上是平衡二叉搜索树的缩写。

二叉搜索树的致命软肋在于它时间复杂度依赖的树高可以被卡到，如果这棵树足够“平衡”，那么树高就会被调整到较为理想的，就像堆那样。

因此我们需要尽可能维持树的平衡，使它的树高维持在级别。

旋转

旋转是平衡树中常用的调整树高的方式，它可以在不影响二叉搜索树性质的前提下改变树的形态。

比如下面这张图，我们想把结点旋转到结点的位置，同时不影响二叉搜索树的性质，怎么办呢？

我们需要保证中序遍历始终为 a y b x c，因此下面是一个可行的目标状态：

我们观察这个过程，发现两张图的区别在于：

y 的右子改为 x。
d 原来 x 的位置被改成 y。
x 的左子改为 b。

我们直接这样改即可。这个操作被称为右旋或 Zig。

void zig(int& p){
    int nf=t[p].ls;
    t[p].ls=t[nf].rs;
    t[nf].rs=p;
    t[nf].siz=t[p].siz;
    pushup(p);pushup(nf);
    p=nf;
}

左旋或 Zag 只需要把这个过程逆向就好了。

void zag(int& p){
    int nf=t[p].rs;
    t[p].rs=t[nf].ls;
    t[nf].ls=p;
    t[nf].siz=t[p].siz;
    pushup(p);pushup(nf);
    p=nf;
}

此外还有一种情况，是我只想要把一个结点旋转到父亲的位置，此时我们直接综合 Zig 和 Zag 两种情况即可。注意这样写要记父亲。

int get(int p){return rs(fa(p))==p;}
void rotate(int x){
    int y=fa(x),z=fa(y),p=get(x);
    if(z)t[z].ch[get(y)]=x;
    t[y].ch[p]=t[x].ch[!p];fa(t[x].ch[!p])=y;
    t[x].ch[!p]=y;fa(y)=x;fa(x)=z;
    pushup(y),pushup(x);
}

p.s. 其实 Zig 和 Zag 也可以合成一个函数：

void rotate(int& p,bool s){
    int nr=t[p].ch[s];
    t[p].ch[s]=t[nr].ch[s^1];
    t[nr].ch[s^1]=p;
    pushup(p);pushup(nr);
    p=nr;
}

Treap

树堆（Tree Heap，简写为 Treap）的思想：给每个点分配一个随机的优先级（priority），需要满足父结点的优先级大于（或小于）子结点。也就是说，Treap 其实是一棵笛卡尔树。

可以证明 Treap 的树高是的。根据实验，个结点的 Treap 的平均树高是左右，大概可以理解为到倍。

Splay

伸展树（Splay Tree）的思想：每访问一个结点，就把这个结点不断旋转到根。

ちょっと待って，我构造一条链不就能卡了，这看起来是假的啊？

事实上 Splay 使用的是一种所谓“双旋”。它分为三种情况：

当前结点的父亲是根。这种情况直接旋转即可。
当前结点与父亲在同一条直线上（即父亲和当前结点要么同为左儿子要么同为右儿子），这种情况下先旋转父亲结点再旋转当前结点。
当前结点与父亲不在同一条直线上，这种情况旋转当前结点两次。

而用了这个看起来非常玄学的“双旋”后，Splay Tree 的时间复杂度降低到了均摊。证明可以参考 OI-Wiki。

其他思想

Treap 和 Splay 是最为常见与实用的平衡树，不过还有一些其他的平衡树。

AVL 树：维护每个结点的最深深度，一旦左右子树的最深深度差高于就旋转。

WBLT：建个点，只在叶结点上挂数，每个结点的权值是其右子的权值，满足右儿子权值大于左儿子。旋转维护平衡。

替罪羊树：维护子树大小，一旦某个子树的大小占比过大就暴力重构。

~~Red Blue Tree~~ 红黑树（Red Black Tree）：最快的平衡树，是 std::map 等的内部实现，通过给结点染色等一系列方式维护树的平衡，但是 OI 里没人写因为实在太复杂了。

实现

旋转 Treap

旋转 Treap 的大部分操作与普通 BST 相同，唯一的区别在于要在访问完一个结点后判断一下是否满足堆性质，不满足就要旋转。

Treap 的删除操作的想法也很暴力：我们不愿意看到待删除结点有两个儿子，那我们把它转到最多一个儿子就好了。

Splay

我们前面提到过，我们在找到一个结点后就把它双旋到根。

其他操作大同小异，这里主要讲一下 Splay 的重要特性：可以断树，这也是它可以用于维护序列的重要特性。

所谓断树，就是把树根据排名或者值分裂为两棵树。

Splay 想实现断树很简单：如果我们要把一棵树分裂为两棵，第一棵的大小为，我们只需要找到排名为的元素将其双旋到根，然后把的右儿子切掉即可。这样第一棵树的大小即为。

而如果我们想把这断掉的两棵树合并在一起也很简单：找到第一棵树最大的元素和第二棵树最小的元素，分别双旋到根，第一棵树的根的右儿子设为第二棵树。

因此对于删除操作，我们把树断成三段，把第一段和第三段合起来就完了。

顺便提一嘴，Splay 树是 Link-Cut Tree 的基础，（据说）是当初 Tarjan 为了把 LCT 的时间复杂度从均摊降到均摊发明的小玩意。~~所以 LCT 用 Treap 也能写啦。。。~~

非旋 Treap（FHQ Treap）

~~学习平衡树不学 FHQ Treap，就像，只能度过一个相对失败的人生。~~

Treap 可以实现维护序列吗？可以的。

FHQ Treap 是一种不需要旋转的平衡树，它只有两个核心操作：split 和 merge。

split：把树按照 rank/key 分成两半。

merge：把两棵树合并。

split

split 的流程如下：

从根结点开始，设我们希望第一棵树的大小为。

如果当前结点为空，直接返回即可。
我们求出当前结点的，即为其左子大小。
如果，说明当前结点应当属于第二棵树，因此当前结点右子都属于第二棵树；而左子内还有一部分属于第二棵树，递归到左子树继续 split，然后把找出的左子树中所有属于第二棵树的结点作为当前结点的左子树。
否则说明当前结点应当属于第一棵树，因此当前结点左子都属于第一棵树；而右子内还有一部分属于第一棵树，递归到右子树继续 split，然后把找出的右子树中所有属于第一棵树的结点作为当前结点的右子树。注意此时我们需要。

void split(int p,int s,int& x,int& y){//当前结点，第一棵树大小，第一棵树的根，第二棵树的根
    if(!p)return void(x=y=0);
    int rk=t[ls(p)].siz+1;
    if(rk<=s){
        x=p;
        split(rs(p),s-rk,rs(p),y);
    }
    else{
        y=p;
        split(ls(p),s,x,ls(p));
    }
    pushup(p);
}

merge

merge 的流程如下：

我们设当先要合并的两棵树分别为。

如果中任意一个为空树，直接返回不是空树的那一个即可。
如果的优先级高于，将与的右子树合并的结果作为新的右子树。
否则将与左子树合并的结果作为新的左子树。

int merge(int x,int y){//两棵要合并的树，返回合并后的根
    if(!x||!y)return x+y;
    if(t[x].pri<t[y].pri){
        rs(x)=merge(rs(x),y);
        return pushup(x),x;
    }
    ls(y)=merge(x,ls(y));
    return pushup(y),y;
}

操作序列

我们可以看出 FHQ Treap 似乎天生就是为了解决序列问题的，它的两个操作恰好就是断树和合并。

因此我们只需要把这个区间 split 出来，在这个区间打上懒标记，合并回去就完事了，剩下的和线段树就差不多了无非就是 pushup pushdown addtag 了。

int x,y,z;
split(rt,l-1,x,y);
split(y,r-l+1,y,z);
// addtag(y,/*你要做的修改*/);
rt=merge(x,merge(y,z));

注意如果涉及区间操作，我们还是需要在访问结点的第一步 pushdown。

模板

在此只提供 FHQ Treap 的模板。

struct node{
    int ch[2],siz,pri;
    /*在这里定义你要维护的信息*/
};
struct Tag{
    /*在这里定义你的标记*/
};
struct treap{
    #define ls(p) t[p].ch[0]
    #define rs(p) t[p].ch[1]
    std::mt19937 rnd;
    private:
        vector<node> t;
        vector<Tag> tag;
        int rt,nt;
        void pu(int p){
            t[p].siz=t[ls(p)].siz+t[rs(p)].siz+1;
            /*在这里定义你的上传方式*/
        }
        void atag(int p,Tag x){
            /*在这里定义你的标记下传*/
        }
        void pd(int p){
            if(ls(p))atag(ls(p),tag[p]);
            if(rs(p))atag(rs(p),tag[p]);
            /*清空标记*/
        }
        void spl(int p,int s,int& x,int& y){
            if(!p)return x=y=0,void();
            pd(p);
            int rk=t[ls(p)].siz+1;
            if(s>=rk)x=p,spl(rs(p),s-rk,rs(x),y);
            else y=p,spl(ls(p),s,x,ls(y));
            pu(p);
        }
        int mrg(int x,int y){
            if(!x||!y)return x+y;
            pd(x),pd(y);
            if(t[x].pri<t[y].pri)return rs(x)=mrg(rs(x),y),pu(x),x;
            return ls(y)=mrg(x,ls(y)),pu(y),y;
        }
        void nnode(/*初始值*/){
            nt++;
            t.push_back((node){{0,0},1,rnd()/*你维护的东西*/});
            tag.push_back({/*tag的初始值*/});
        }
    public:
        treap(int _seed=188716):rnd(_seed),t(1),tag(1),nt(0){}
        void push_back(/*你要在后面加的值*/){
            nnode(/*你要加入的值*/);
            rt=mrg(rt,nt);
        }
        void ins(int pos/*,你要插入的值*/){
            nnode(/*你要加入的值*/);
            int x,y;
            spl(rt,pos,x,y);
            rt=mrg(x,mrg(nt,y));
        }
        void mdf(int l,int r){
            int x,y,z;
            spl(rt,l-1,x,y);
            spl(y,r-l+1,y,z);
            atag(y,(Tag){/*你要做的修改*/});
            rt=mrg(x,mrg(y,z));
        }
        node qry(int l,int r){
            int x,y,z;
            spl(rt,l-1,x,y);
            spl(y,r-l+1,y,z);
            node ans=t[y];
            rt=mrg(x,mrg(y,z));
            return ans;
        }
    #undef ls
    #undef rs
};

比较

	旋转 Treap	FHQ Treap	Splay
结点信息	儿子，子树大小，优先级	儿子，子树大小，优先级	儿子，父亲，子树大小
常数大小	小	大	中
能否维护序列	否	是	是
代码难度（个人）	中	小	中
特殊	-	-	用它写 LCT 的时间复杂度降到均摊

STL

`std::set/map`

set 是一个基于红黑树实现的集合，支持以下操作：

insert：插入一个元素。。
erase：删除一个元素。。
lower_bound：查询不小于某个元素的最小值。。
upper_bound：查询大于某个元素的最小值。。
*begin：查询最小值。。
*rbegin：查询最大值。。

如果开一个迭代器遍历一个 set 将按照大小升序。

map 与 set 类似，区别在于 map 中每一个元素都有两个值 key 和 value，排序时按照 key 排序。此外 map 重载了 [] 符号，可以通过类似于 mp["Friday"]=5 的方式进行访问。

如果在 map 或 set 前加上 multi 前缀，则可以同时插入多个 key 相同的元素，但是请注意如果多个元素只需要删除一个只能删迭代器不能删值。别问我怎么知道的，问就是 NOIP2018 D1T3。

`__gnu_pbds::tree`

__gnu_pbds::tree 也是一棵红黑树，相较于 set/map 而言多了两个功能：

find_by_order：查询 Kth。
order_of_key：查询 rank。

只不过这个东西的定义有亿点麻烦。

#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
typedef tree<int,null_type,std::less<int>,rb_tree_tag,tree_order_statistics_node_update> Set;
typedef tree<int,int,std::less<int>,rb_tree_tag,tree_order_statistics_node_update> Map;

Set s;
Map m;

高级

可并堆

操作

维护一系列集合，每个集合初始有一个元素。支持：

合并两个集合。
查询某集合的最小值。
删除某集合的最小值。

思想

~~可并堆其实就是...并查集和堆的孩子。~~

可并堆也是一棵二叉树，并且也满足结点权值不大于其父亲。

我们直接来看可并堆的核心操作：合并两集合。

合并

我们设要合并结点标号为的两二叉树。

如果任意一棵树为空树，返回不为空的那一棵即可。
否则将中权值较小的结点作为新根，并任意选择新根的一个儿子与权值较大的结点合并。

这一点非常像 FHQ Treap。

查询

我们记录每个结点所在树的根结点，然后在查询时暴力跳根结点。

...是不可能的。

我们需要路径压缩。

删除

合并待删除结点的左右儿子即可。

优化

ちょっと待って，这个时间复杂度看起来是树高相关的可以卡到的啊？

这里有三个优化：

左偏树

我们首先指定合并时都往右子树合并，此时影响时间复杂度的就变成了右链的长度，设其为。

左偏树在满足可并堆性质的同时还满足，也就是左儿子的右链长度不小于右儿子的右链长度。

在这种情况下，个结点的左偏树的右链长度不超过，在树为完全二叉树卡满，可以自行画图理解。

我们在合并时向右子树合并，但是合并完成后可能右子树的右链长度大于左子树了，此时就需要交换左右子树。

右链长度可以动态维护。

左偏树的深度没有保证，一条向左的链也是左偏树，因此您还是需要写路径压缩 :D

~~其实您也可以指定向左子树合并并维护左链长度，右子树左链长度大于左子树，于是您发明了右偏树 :D~~

下图是一个左偏树的例子（结点上的蓝色数字是右链长度）：

随机合并

如题。

斜堆

和左偏树一样，唯一的区别在于我们不记录，而是在合并后直接交换左右儿子。

时间复杂度是均摊的。证明可以参考这里。

模板

struct lft{//左偏树
    #define ls(p) t[p].ch[0]
    #define rs(p) t[p].ch[1]
    struct node{
        int ch[2],val,h;
        bool del;
        node(int _val=0):ch({0,0}),val(_val),h(0),del(0){}
    };
    private:
        vector<node> t;
        vi rt;
        int find(int x){return x==rt[x]?x:rt[x]=find(rt[x]);}
        int mrg(int x,int y){
            if(!x||!y)return t[x+y].h=0,x+y;
            if(t[x].val>t[y].val||(t[x].val==t[y].val&&x>y))std::swap(x,y);
            rs(x)=mrg(rs(x),y);
            if(t[rs(x)].h>t[ls(x)].h)std::swap(ls(x),rs(x));
            t[x].h=t[rs(x)].h+1;
            return x;
        }
    public:
        lft(int n=0,vi a={}):t(n+1),rt(n+1){for(int i=1;i<=n;++i)rt[i]=i,t[i].val=a[i];}
        void merge(int x,int y){
            if(t[x].del||t[y].del)return;
            x=find(x),y=find(y);
            if(x!=y)rt[x]=rt[y]=mrg(x,y);
        }
        int pop(int x){
            if(t[x].del)return -1;
            x=find(x);
            t[x].del=1;
            rt[ls(x)]=rt[rs(x)]=rt[x]=mrg(ls(x),rs(x));
            ls(x)=rs(x)=t[x].h=0;
            return t[x].val;
        }
    #undef ls
    #undef rs
};

const int M=1e5+5;
namespace skew_heap{//斜堆，远古马蜂丑勿喷QAQ
    struct node{
        int f,l,r,v;
        bool SPFA;
    }heap[M];
    int find(int x){return heap[x].f==x?x:heap[x].f=find(heap[x].f);}
    int merge(int x,int y){
        if(!(~x))return y;
        if(!(~y))return x;
        if(heap[x].v>heap[y].v||(heap[x].v==heap[y].v&&x>y))std::swap(x,y);
        int nr=merge(heap[x].r,y);
        heap[nr].f=x;heap[x].r=nr;
        std::swap(heap[x].l,heap[x].r);
        return x;
    }
    int top(int x){
        if(heap[x].SPFA)return -1;
        x=find(x);
        return heap[x].v;
    }
    void pop(int x){
        if(heap[x].SPFA)return;
        x=find(x);
        heap[x].SPFA=1;
        heap[heap[x].l].f=heap[x].l;heap[heap[x].r].f=heap[x].r;
        heap[x].f=merge(heap[x].l,heap[x].r);
    }
}

线段树合并

操作

合并两棵权值线段树。时间复杂度取决于两线段树上重合的结点数，但是如果所有要合并的树中插入的数总和在左右那么时间复杂度大概在。

思想

我们设要合并根结点分别为与的线段树。

如果与中任意一个为空，返回不为空的即可。
如果与是叶结点，直接合并即可。
否则分别合并的左子和右子，然后执行 pushup。

线段树合并分两种：一种是新开合并得到的结点，一种是把一棵树的信息直接加到另一棵树上。前者不会破坏原树，后者省空间。

时间复杂度分析

合并两棵满线段树的时间复杂度是，但是实际上待合并的结点总数是级别，而一个结点一般不会被合并两次，因此时间复杂度。

模板

//保留原树信息的写法
int mrg(int x,int y,int s,int t){
    if(!x||!y)return x+y;
    if(s==t){
        int p=++nt;
        t[p]=/*合并x,y的信息*/;
        return p;
    }
    int p=++nt;
    ls(p)=mrg(ls(x),ls(y),s,mid);
    rs(p)=mrg(rs(x),rs(y),mid+1,t);
    return pushup(p),p;
}
//省空间的写法
void mrg(int &x,int &y,int s,int t){
    if(!x||!y){x+=y;return;}
    if(s==t){
        /*把y并到x上*/
        return;
    }
    mrg(ls(x),ls(y),s,mid);
    mrg(rs(x),rs(y),mid+1,t);
    pushup(x);
}

李超线段树

操作

Luogu4097 【模板】李超线段树 / [HEOI2013] Segment

要求在平面直角坐标系下进行两个操作：

在平面上加入一条线段。记第条被插入的线段的标号为。

给定一个数，询问与直线相交的线段中，交点纵坐标最大的线段的编号。

强制在线，操作数。

李超线段树是一个时间复杂度的数据结构，支持动态维护线段，也不失为一个正面强攻维护半平面交的好方法。

思想

李超线段树基于标记永久化思想，即标记是直接被修改的对象。

我们在线段树的每个结点上记录的是它管辖的区间的上最优的线段。

对于一次修改操作，我们需要分类讨论当前结点最优线段和待插入线段。

在优于。
1. 在优于：说明可能在当前区间左子树可能会成为更优解。将传到左子树继续修改。
2. 在优于：说明可能在当前区间右子树可能会成为更优解。将传到右子树继续修改。
  
  以上两种情况不可能同时触发，否则在一定不优。
在不优。直接交换，然后跳到 1。

我们考虑线段实质上是一次函数，因此方便求解在各个位置的值。

对于查询操作，我们需要将查询路径上所有结点的答案都算上（因为它们都包含了查询位置）。

时间复杂度分析

每次访问个区间，而每个待修改区间都最多向下递归层，因此单次修改时间复杂度。

模板

const double eps=1e-10;
struct seg{double k,b;int id;};
double calc(seg l,int x){return l.k*x+l.b;}
int chk(double x,double y){//三元比较函数，优化精度
    if(fabs(x-y)<eps)return 0;
    if(x>y)return 1;
    return -1;
}
struct lct{//不是Link-Cut Tree哦:D
    #define ls (p<<1)
    #define rs ((p<<1)|1)
    #define mid ((s+t)>>1)
    private:
        vector<seg> T;
        int n;
        void upd(seg x,int p,int s,int t){
            seg &y=T[p];
            if(chk(calc(x,mid),calc(y,mid))>0)std::swap(x,y);
            int l=chk(calc(x,s),calc(y,s)),r=chk(calc(x,t),calc(y,t));
            if(l>0||(!l&&x.id<y.id))upd(x,ls,s,mid);
            if(r>0||(!r&&x.id<y.id))upd(x,rs,mid+1,t);
        }
    public:
        lct(int _n){T.resize((n=_n)*4+50,(seg){0,-1e9,0x3f3f3f3f});}
        void ins(int l,int r,seg x){
            std::function<void(int,int,int)> md=[&](int p,int s,int t){
                if(l>t||s>r)return;
                if(l<=s&&t<=r)return upd(x,p,s,t);
                md(ls,s,mid),md(rs,mid+1,t);
            };md(1,1,n);
        }
        int qry(int pos){//此处是查编号，查最大值更短
            std::function<seg(int,int,int)> qr=[&](int p,int s,int t){
                seg ans=T[p];
                if(s==t)return ans;
                seg q=(pos<=mid?qr(ls,s,mid):qr(rs,mid+1,t));
                int o=chk(calc(ans,pos),calc(q,pos));
                if(o<0||(!o&&ans.id>q.id))ans=q;
                return ans;
            };
            int ans=qr(1,1,n).id;
            if(ans==0x3f3f3f3f)ans=0;
            return ans;
        }
};

势能线段树（吉司机线段树）

操作

LibreOJ 6565 最假女选手

Luogu6242 线段树3

UOJ164 【清华集训2015】V

时间复杂度的区间 chkmax/chkmin，区间历史和。

（2025/5/26:复杂度下界可以证明是的，但其实这个算法跑得更像）

思想

关于区间 chkmax、区间求和、RMQ

在结点上维护区间最大值、次大值、最大值个数。

如果要 chkmax 的值大于最大值，直接更改即可。
如果要 chkmax 的值不大于最大值但是不小于次大值，对最大值与和进行影响。
否则向下递归合并。

时间复杂度。

证明、关于历史最大值以及一车其他东西

问我干嘛。

代码

struct sgb{
    int mx,sx,cx;
    int mn,sn,cn;
    ll sum,ta;
    int tx,tn;
    sgb(int x=0):mx(x),sx(-inf),cx(1),mn(x),sn(inf),cn(1),sum(x),ta(0),tx(inf),tn(-inf){}
};

struct SGB{
    #define ls ((p<<1))
    #define rs ((p<<1)|1)
    #define mid ((s+t)>>1)
    private:
        vector<sgb> T;
        int n;
        function<void(int,int,int)> dfs;
        void pu(int p){
            auto &l=T[ls],&r=T[rs],&x=T[p];
            x.sum=l.sum+r.sum;
            x.mx=max(l.mx,r.mx);
            x.sx=
                (l.mx==r.mx?
                    max(l.sx,r.sx):
                    (x.mx==l.mx?max(l.sx,r.mx):max(l.mx,r.sx))
                );
            x.cx=(l.mx==r.mx?l.cx+r.cx:(x.mx==l.mx?l.cx:r.cx));
            x.mn=min(l.mn,r.mn);
            x.sn=
                (l.mn==r.mn?
                    min(l.sn,r.sn):
                    (x.mn==l.mn?min(l.sn,r.mn):min(l.mn,r.sn))
                );
            x.cn=(l.mn==r.mn?l.cn+r.cn:(x.mn==l.mn?l.cn:r.cn));
        }
        void add(int p,int s,int t,ll x){
            T[p].sum+=x*(t-s+1);
            T[p].mx+=x;T[p].sx+=x;T[p].tx+=x;
            T[p].mn+=x;T[p].sn+=x;T[p].tn+=x;
            T[p].ta+=x;
        }
        void ckmax(int p,int x){
            if(T[p].mn>=x)return;
            T[p].sum+=1ll*(x-T[p].mn)*T[p].cn;
            if(T[p].mn==T[p].mx)T[p].mx=x;
            else if(T[p].sx==T[p].mn)T[p].sx=x;
            T[p].mn=T[p].tn=x;
            if(T[p].tx<x)T[p].tx=x;
        }
        void ckmin(int p,int x){
            if(T[p].mx<=x)return;
            T[p].sum-=1ll*(T[p].mx-x)*T[p].cx;
            if(T[p].mn==T[p].mx)T[p].mn=x;
            else if(T[p].sn==T[p].mx)T[p].sn=x;
            T[p].mx=T[p].tx=x;
            if(T[p].tn>x)T[p].tn=x;
        }
        void pd(int p,int s,int t){
            if(T[p].ta){
                add(ls,s,mid,T[p].ta),add(rs,mid+1,t,T[p].ta);
                T[p].ta=0;
            }
            if(T[p].tx!=inf){
                ckmin(ls,T[p].tx),ckmin(rs,T[p].tx);
                T[p].tx=inf;
            }
            if(T[p].tn!=-inf){
                ckmax(ls,T[p].tn),ckmax(rs,T[p].tn);
                T[p].tn=-inf;
            }
        }
    public:
        SGB(int _n,vi a):n(_n),T(_n*4+10){
            dfs=[&](int p,int s,int t){
                if(s==t)return T[p]=sgb(a[s]),void();
                dfs(ls,s,mid),dfs(rs,mid+1,t),pu(p);
            };dfs(1,1,n);
        }
        void chkmax(int l,int r,int x){
            dfs=[&](int p,int s,int t){
                if(l>t||s>r||T[p].mn>=x)return;
                if(l<=s&&t<=r&&T[p].sn>x)return ckmax(p,x);
                pd(p,s,t),dfs(ls,s,mid),dfs(rs,mid+1,t),pu(p);
            };dfs(1,1,n);
        }
        void chkmin(int l,int r,int x){
            dfs=[&](int p,int s,int t){
                if(l>t||s>r||T[p].mx<=x)return;
                if(l<=s&&t<=r&&T[p].sx<x)return ckmin(p,x);
                pd(p,s,t),dfs(ls,s,mid),dfs(rs,mid+1,t),pu(p);
            };dfs(1,1,n);
        }
        void Add(int l,int r,int x){
            dfs=[&](int p,int s,int t){
                if(l>t||s>r)return;
                if(l<=s&&t<=r)return add(p,s,t,x);
                pd(p,s,t),dfs(ls,s,mid),dfs(rs,mid+1,t),pu(p);
            };dfs(1,1,n);
        }
        ll qry_sum(int l,int r){
            ll ans=0;
            dfs=[&](int p,int s,int t){
                if(l>t||s>r)return;
                if(l<=s&&t<=r)return ans+=T[p].sum,void();
                pd(p,s,t),dfs(ls,s,mid),dfs(rs,mid+1,t);
            };dfs(1,1,n);return ans;
        }
        int qry_max(int l,int r){
            int ans=-inf;
            dfs=[&](int p,int s,int t){
                if(l>t||s>r)return;
                if(l<=s&&t<=r)return cmax(ans,T[p].mx);
                pd(p,s,t),dfs(ls,s,mid),dfs(rs,mid+1,t);
            };dfs(1,1,n);return ans;
        }
        int qry_min(int l,int r){
            int ans=inf;
            dfs=[&](int p,int s,int t){
                if(l>t||s>r)return;
                if(l<=s&&t<=r)return cmin(ans,T[p].mn);
                pd(p,s,t),dfs(ls,s,mid),dfs(rs,mid+1,t);
            };dfs(1,1,n);return ans;
        }
    #undef ls
    #undef rs
    #undef mid
};

可持久化数据结构

操作

查询历史版本。

在可持久化时，我们将每次修改都作为一个新的版本，它是基于之前的某个版本修改而来。

可持久化分为两种：历史版本只读、历史版本可以修改。

思想

朴素的思想是每个版本都暴力开一个数据结构，但是这样时间空间会一起爆炸。

我们发现像线段树、平衡树、Trie 等数据结构，对其进行修改时真正会影响到的结点较少，因此我们考虑结点的复用。

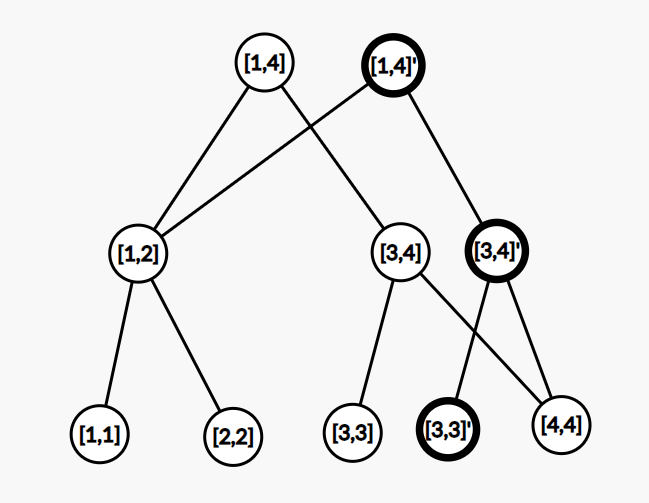
以单点修改线段树为例。假设我们要修改下图中的位置：

那么我们需要修改的结点只有，剩下的都不用改。

那么我们就可以这样新建一个新的版本：

加粗的结点是新版本新建的点。

这样，如果我们要在新版本上搞事情，只需要从结点开始遍历即可，这样得到的和新开一棵树的结果一致。我们称它为一个版本的根。

可持久化数据结构可以做标记下传，但是在下传时要开新的点否则会把树废掉。

可持久化 Trie 与线段树类似，都是新开一个根然后大量复用。

可持久化平衡树一般用 FHQ Treap，因为它的分裂过程也是一条链，影响的只有这条链上的结点，把这些结点复制即可。

主席树

主席树，正式名称“可持久化权值线段树”，不要了解为啥叫这个。

主席树一般用于解决有关区间 K 小相关的问题。

思想

如果我们要做区间 K 小，朴素的想法是开棵权值线段树然后在第棵与第棵树上二分，但是这样会炸。

我们此时用可持久化思想，版本表示区间的权值线段树。由于每个版本只需要修改一个位置正确性成立。

这样只需要在版本和版本上二分就好了。

记得先离散化。

模板

远古马蜂丑勿喷。

//Luogu3319
namespace psgt{
    int cnt,rt[M];
    int ls[M*20],rs[M*20],val[M*20];
    void build(int &pos,int s,int t){
        pos=++cnt;
        if(s==t){val[pos]=a[s];return;}
        int mid=s+t>>1;
        build(ls[pos],s,mid);build(rs[pos],mid+1,t);
    }
    void insert(int &pos,int ver,int q,int x,int s=1,int t=n){
        pos=++cnt;ls[pos]=ls[ver];rs[pos]=rs[ver];val[pos]=val[ver];
        if(s==t){val[pos]=x;return;}
        int mid=s+t>>1;
        if(q<=mid)insert(ls[pos],ls[ver],q,x,s,mid);
        else insert(rs[pos],rs[ver],q,x,mid+1,t);
    }
    int query(int pos,int q,int s=1,int t=n){
        if(s==t)return val[pos];
        int mid=s+t>>1;
        if(q<=mid)return query(ls[pos],q,s,mid);
        else return query(rs[pos],q,mid+1,t);
    }
}

//Luogu3834
int n,L,m,a[M],X[M],rt[M];
#define ls(p) ch[p][0]
#define rs(p) ch[p][1]
#define mid ((s+t)>>1)
int ch[M<<5][2],cnt[M<<5],nt;
void ins(int ver,int val,int &p,int s=1,int t=L){
    p=++nt;ls(p)=ls(ver);rs(p)=rs(ver);cnt[p]=cnt[ver]+1;
    if(s==t)return;
    if(val<=mid)ins(ls(ver),val,ls(p),s,mid);
    else ins(rs(ver),val,rs(p),mid+1,t);
}
int qry(int k,int l,int r,int s=1,int t=L){
    if(s==t)return X[s];
    int rk=cnt[ls(r)]-cnt[ls(l)];
    if(k<=rk)return qry(k,ls(l),ls(r),s,mid);
    else return qry(k-rk,rs(l),rs(r),mid+1,t);
}

分块

操作

有些操作用普通的分治数据结构可能不好做，比如区间加区间比某个数小的数个数，这时候就可以用分块了。

分块的时间复杂度一般和根号相关。

思想

分块顾名思义就是将序列分为若干个块，统一维护这一整个块的信息。

在区间操作时，我们可以把这个操作区间分为整块和散块。顾名思义，整块就是一整个的块，散块就是不完整的块。容易证明只有头尾两个块可能是散块。

在修改时，我们对整块打上标记，然后对散块暴力修改并重构。

设块长（每个块的长度）为，那么整块的数量量是的，因此单次操作时间复杂度是的。

容易证明在时最优，时间复杂度。

如果整块修改和散块修改的时间复杂度不同，则需要对块长进一步讨论。不过由于各种玄学问题，理论最优块长可能不同于实际最优块长。

例题可以去做一下区间众数、弹飞绵羊。

ODT（颜色段均摊）

珂朵莉树（Old_Driver Tree,ODT）并不是一个数据结构而是一个骗分算法。起源 CF896C，由 lxl 提出。

操作

随便，但是必须包含区间推平（区间赋值）。

只能在数据随机时使用

思想

ODT 的思想非常暴力：把序列分成若干个块，每个块内所有值相同。

此时我们发现：区间赋值操作实质是把若干个块合并在一起，其他的修改操作实质是把块分裂，于是我们只需要快速进行这两个操作就好了。显然二分即可。

至于查询操作，暴力跳块就好了。

实现一般用 std::set 并定义块为结构体记录其左右界和值。

时间复杂度

在数据随机的情况下，时间复杂度。

模板

https://codeforces.com/contest/896/submission/233049186

树套树

有时候我们遇到的问题用单一数据结构难以维护，此时就可以用嵌套数据结构了。

常见的有线段树套线段树、线段树套平衡树、BIT 套主席树、分块套 BIT 等。BIT 套 BIT 就是二维 BIT。

由于这类题比较少，在此不作详细介绍。

树链剖分

（这确实不是数据结构的内容，但是如果不放就没办法写 LCT，所以还是放一下吧 xD）

顾名思义，树链剖分就是要把树解剖成一条一条的链，然后把树上问题转换为区间问题，使用线段树等数据结构求解。

OI 中一般采取轻重链剖分。

几个概念：

轻、重儿子：一个结点中的所有儿子中，子树大小最大的儿子为重儿子，其余为轻儿子。

轻、重边：连接父结点到重儿子的边叫做重边，连接父结点到轻儿子的边叫做轻边。

重链：由多条重边连接而成的路径。特别的，不在其他重链上的单个节点也算一条重链。

维护内容

dep：结点的深度。

dfn：结点的 dfs 序。

rnk：记录 dfs 序的第几位是几号结点。（一般用于建线段树）

fa：结点的父亲。

top：这个结点所在重链的链顶（深度最小的点）。

siz：子树大小

son：重儿子的编号。

预处理

使用树剖要首先做两次 dfs。

第一次：处理出每个结点的父亲、重儿子、子树大小、深度。

第二次：处理出每个结点的 dfs 序、rnk、链顶。注意先走重儿子方便处理重链。

操作

所有的结点都有唯一一条重链与之对应，那么这意味着一条路径可以被拆成多条路径，每一条路径都只被一条重链包含。

考虑为什么我们要在标 dfn 的时候先走重儿子：这样处理之后每条重链在 dfs 序上就是连续的一段了，从 top 向下递增。

那么我们就可以设计以下算法：

从两个查询的结点一直向上跳，每一次跳跃选取链顶深度较大的一个查询/修改对应重链链顶到这个点的区间和/执行区间加操作并跳到这条链链顶的父亲，直到跳到同一条重链上，再加上/修改剩下的一部分。

（本来这里有几张华丽的图片的，但是被可恶的图床吃了）

时间复杂度分析

注意到跳跃的次数=执行修改/查询的次数=轻边的条数，而轻边的条数为。证明：每走一条轻边，子树大小至少减半（否则根据定义它就不是轻边）。

因此总时间复杂度为，其中是选用数据结构的单次操作时间复杂度。比如若使用线段树维护，时间复杂度为。

闲话：如果存在一种数据结构，满足可以查询前缀、查询区间，那么此时总时间复杂度为（因为本质是次重链的前缀查询和一次区间查询）。

模板

//远古马蜂丑勿喷
#include<cstdio>
#define int long long
const int M=1e5+5;
inline int read(){int x(0),op(0);char ch=getchar();while(ch<'0'||ch>'9')op|=(ch==45),ch=getchar();while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();return op?-x:x;}
int n,m,r,P;
int a[M];
struct edge{
    int v,nxt;
}e[M<<1];
int h[M],etot;
void adde(int u,int v){e[++etot]=(edge){v,h[u]};h[u]=etot;}
namespace HLD{
    int fa[M],siz[M],hson[M],dfn[M],top[M],rnk[M],dep[M];
    int DFN;
    void dfs1(int x,int f){
        dep[x]=dep[f]+1;siz[x]=1;hson[x]=0;fa[x]=f;
        for(int i=h[x],v;v=e[i].v,i;i=e[i].nxt)if(v!=f){
            dfs1(v,x);siz[x]+=siz[v];
            if(siz[hson[x]]<siz[v])hson[x]=v;
        }
    }
    void dfs2(int x,int tp){
        dfn[x]=++DFN;rnk[DFN]=x;top[x]=tp;
        if(hson[x])dfs2(hson[x],tp);
        for(int i=h[x],v;v=e[i].v,i;i=e[i].nxt)if(v!=fa[x]&&v!=hson[x])dfs2(v,v);
    }
    namespace SGT{
        #define LS (p<<1)
        #define RS ((p<<1)|1)
        #define MID ((s+t)>>1)
        int T[M<<2],tag[M<<2];
        void pushup(int p){T[p]=(T[LS]+T[RS])%P;}
        void pushdown(int p,int s,int t){
            if(tag[p]){
                T[LS]=(T[LS]+(tag[p]*(MID-s+1))%P)%P;T[RS]=(T[RS]+(tag[p]*(t-MID))%P)%P;
                tag[LS]=(tag[LS]+tag[p])%P;tag[RS]=(tag[RS]+tag[p])%P;
            }
            tag[p]=0;
        }
        void build(int p=1,int s=1,int t=n){
            if(s==t){
                T[p]=a[rnk[s]];
                return;
            }
            build(LS,s,MID);build(RS,MID+1,t);
            pushup(p);
        }
        int query(int l,int r,int p=1,int s=1,int t=n){
            if(t<l||r<s)return 0;
            if(l<=s&&t<=r)return T[p];
            pushdown(p,s,t);
            return (query(l,r,LS,s,MID)+query(l,r,RS,MID+1,t))%P;
        }
        void modify(int l,int r,int x,int p=1,int s=1,int t=n){
            if(t<l||r<s)return;
            if(l<=s&&t<=r){
                T[p]=(T[p]+(t-s+1)*x%P)%P;
                tag[p]=(tag[p]+x)%P;
                return;
            }
            pushdown(p,s,t);
            modify(l,r,x,LS,s,MID);modify(l,r,x,RS,MID+1,t);
            pushup(p);
        }
    }
    void init(){dfs1(r,0);dfs2(r,r);SGT::build();}
    void modifych(int u,int v,int x){
        while(top[u]!=top[v]){
            if(dep[top[u]]<dep[top[v]])std::swap(u,v);
            SGT::modify(dfn[top[u]],dfn[u],x);u=fa[top[u]];
        }
        if(dep[u]>dep[v])std::swap(u,v);
        SGT::modify(dfn[u],dfn[v],x);
    }
    void modifysub(int p,int x){
        SGT::modify(dfn[p],dfn[p]+siz[p]-1,x);
    }
    int querych(int u,int v){
        int ans=0;
        while(top[u]!=top[v]){
            if(dep[top[u]]<dep[top[v]])std::swap(u,v);
            ans=(ans+SGT::query(dfn[top[u]],dfn[u])%P)%P;u=fa[top[u]];
        }
        if(dep[u]>dep[v])std::swap(u,v);
        ans=(ans+SGT::query(dfn[u],dfn[v])%P)%P;
        return ans;
    }
    int querysub(int p){
        return SGT::query(dfn[p],dfn[p]+siz[p]-1);
    }
}
signed main(){
    n=read(),m=read(),r=read(),P=read();
    for(int i=1;i<=n;++i)a[i]=read();
    for(int i=1;i<n;++i){
        int u=read(),v=read();
        adde(u,v);adde(v,u);
    }
    HLD::init();
    while(m--){
        int op=read(),u=read();
        if(op<4){
            int v=read();
            if(op==1){
                int x=read();
                HLD::modifych(u,v,x);
            }
            else if(op==2){
                printf("%lld\n",HLD::querych(u,v));
            }
            else HLD::modifysub(u,v);
        }
        else printf("%lld\n",HLD::querysub(u));
    }
    return 0;
}

LCT

Link Cut Tree，简称 LCT，是一种可以在巨大常数时间复杂度下解决动态树问题和链操作的数据结构。

动态树问题，即涉及到树的形态发生改变的问题，操作有断边和连边（保证无论如何不会出现环即可）。

思想

LCT 本质还是维护若干条链，和树剖不同的地方就在于树剖维护的是静态树的重链，而 LCT 维护的是所谓“实链”，它甚至可能是单向的任意链。

实链是啥？

我们先引入一个概念：辅助树。

我们希望原树能够用一棵等价的、易于维护的树表示，于是我们参照树剖的思路还是维护若干条链，这些链不需要满足什么特殊要求，我们只希望它能够快速的动起来、连起来、裂开来，那么就可以很自然的想到用多棵平衡树（一般为 Splay 树）以深度为关键字维护；这些被维护的链就被称为实链，实链中的边被称为实边，和树剖中的重链和重边的意义差不多，于是我们自然而然将这一种剖分命名为实链剖分。

上述的平衡树森林并不是完整的辅助树，毕竟原树中还有若干条不在实链上的边，这些边我们称为虚边（和树剖中轻边差不多）。我们为了在辅助树中表示这些虚边，直接强制平衡树必须又记父亲又记儿子。这样的好处在于这些虚边可以通过“记了父亲，父亲不认”的方式来判断，这样也不会影响平衡树的维护。

根据辅助树的定义，我们可以得出一个显而易见的结论：每一棵平衡树里只存在一个点它的父亲不认它（不然成环了），而它一定是这颗平衡树的根，根据这一点我们就可以判断这个结点是不是某棵子平衡树的根。

（注：下文中所有 splay 均代指将一个结点旋转到根，不特指 Splay 树的 splay 操作）

操作

LCT 的核心为 access 操作，它的功能为指定一个点 u，然后将 u 到辅助树根的所有边变成实边并放到同一棵平衡树里。

分析一下这个过程：

我们显然只需要把虚边拉通即可。考虑这样做在辅助树中的意义：找到虚边的父亲 f，然后把 f 所在平衡树中深度大于 f 的结点丢掉换成 u 所在平衡树即可。

因此可以设计下列过程：

将 u 旋转到它所在平衡树的根，此时自动出现 u-f 的虚边。
将 f 旋转到它所在平衡树的根，此时 f 左子树为深度小于它的结点，右子树为深度大于它的结点。
将 f 的右子改为 u。注意到此时 u 以及其子树是一棵合法的平衡树，因此平衡树的性质并未破坏。
进行完上述操作后，如果 f 已经是辅助树根，停止；否则 f 到父亲的虚边即为下一步操作需要拉通的虚边（因为此时 f 在平衡树根上），令 u<-f，回到 2。

实现时对上述过程进行了一定的变形，伪代码表示如下：

access(u):
    v=0
    while(u 不是辅助树根)
        将 u 旋转到平衡树根
        u.右子=v
        v=u
        u=u.父亲

变形的内容是增加了“第零次操作”，即断掉 u 下方的实边。这样做的好处除了使代码更加简洁以外还有方便取出指定的链。

其他操作均可通过 access 实现，如下：

makeroot：把 u 所在原树的根改为 u。首先 access(u)，那么 u 下方的链就断掉了，再 splay(u)，此时 u 是这棵平衡树的最后一个结点同时也是根节点；于是我们在这个结点上打上翻转标记，u 就成了第一个结点了。

（由于 makeroot 操作涉及修改根，故 LCT 大部分情况下只维护无根树）

split：给定结点 u,v，取出 u,v 之间的链。首先 makeroot(u)，随后 access(v)，此时 u,v 就被放在了同一棵平衡树中。为了方便操作，一般还要 splay(v)，随后可以对 v 进行各种平衡树操作。

link：在 u,v 之间连边。理论只需 access(u),splay(u),连接虚边即可，但有些题目喜欢声明“已经联通则无需连接”，而特判又很麻烦，因此一般采用 makeroot(u),access(v),splay(v),连接虚边。

证明：如果 u,v 已经连通，那么前三个操作相当于 split。由于 u 是深度最小的结点而 v 是深度最大的结点，那么根据平衡树的性质此时 u 的父亲必定是 v。

cut：切除 u,v 之间的边。理论只需 split(u,v) 然后断 v 左儿子即可。但有些题目喜欢声明“不存在则忽略”，此时需要判定：u 是否没有右儿子（即 u-v 路径上是否存在其他点），v 的左儿子是否为 u（即 u,v 是否连通）。

时间复杂度略证

根据轻重剖分每条边到根的轻边条数为期望条，再考虑我们每走一次虚边都会把它变成实边并且产生一条新的虚边，因此虚边条数总是均摊的。

我们直接考虑最坏的情况，就是棵高度为的树首尾相连，这样其他平衡树就会变成的树高。

但是 Splay 会把沿途所有树的根直接串起来（画图可知），于是树高变成了，于是 Splay 实现 LCT 的均摊复杂度是。

此外由于 access 操作本身就需求将指定节点旋转到根，故 Splay 具有先天优势。

（闲话：事实上据说 Tarjan 是先发明了 LCT 再发明了 Splay）

模板

struct LCT{
    #define ls(p) t[p].ch[0]
    #define rs(p) t[p].ch[1]
    #define fa(p) t[p].f
    struct node{
        int ch[2],f,v,x,r;
        node():f(0),v(0),x(0),r(0){ch[0]=ch[1]=0;}
    };
    private:
        vector<node> t;
        void pu(int p){t[p].x=t[ls(p)].x^t[rs(p)].x^t[p].v;}
        void d(int p){swap(ls(p),rs(p)),t[p].r^=1;}
        void pd(int p){if(t[p].r){if(ls(p))d(ls(p));if(rs(p))d(rs(p));t[p].r=0;}}
        int ch(int p){return rs(fa(p))==p;}
        bool ir(int p){return !(ls(fa(p))==p||rs(fa(p))==p);}
        void r(int x){
            int y=fa(x),z=fa(y),o=ch(x);
            pd(y),pd(x);
            if(!ir(y))t[z].ch[ch(y)]=x;
            t[y].ch[o]=t[x].ch[o^1];fa(t[x].ch[o^1])=y;
            fa(y)=x;t[x].ch[o^1]=y;fa(x)=z;
            pu(y);pu(x);
        }
        void ud(int p){if(!ir(p))ud(fa(p));pd(p);}
        void s(int x){ud(x);for(int y;y=fa(x),!ir(x);r(x))if(!ir(y))r(ch(y)==ch(x)?y:x);}
        void a(int x){for(int y=0;x;x=fa(x))s(x),rs(x)=y,pu(y=x);}
        void mr(int x){a(x),s(x),d(x);}
        void sp(int u,int v){mr(u),a(v),s(v);}
    public:
        LCT(int n):t(n+1){}
        void m(int p,int x){a(p),s(p),t[p].v=x,pu(p);}
        int q(int u,int v){return sp(u,v),t[v].x;}
        void l(int u,int v){sp(u,v),fa(u)=v;}
        void c(int u,int v){sp(u,v);if(ls(v)==u&&!rs(u))fa(u)=ls(v)=0;}
    #undef ls
    #undef rs
    #undef fa
};

离线算法

~~好了终于到这篇文章的末尾了累死我了~~

上文介绍的所有算法其实都是在线算法，但是有些题目没有强制在线，而在线算法又难以解决。

这时候就可以用离线算法了。

CDQ 分治

回忆一下逆序对的做法，我们在分治时把逆序对分为“跨过区间中点”和“不跨过区间中点”两种，于是我们只需要统计跨过区间中点的逆序对数即可。

这也是 CDQ 分治的统一解法：计算跨过中点的答案，然后递归到两边继续。

CDQ 分治的应用包括但不限于多维偏序等，此外也经常用来做决策单调性 DP。

扫描线

正交范围

在一个 B 维直角坐标系下，第维坐标在之间，内部的点集被称为正交范围。

一般维正交范围简称区间，维正交范围简称矩形，维正交范围简称立方体。

Side

对于 B 维正交范围，每一维都有两个限制，也就是有两个边界（Side），这被称为一个 2B-Side 的 B 维正交范围。

有时候有些维只有一个限制。如果有些维没有限制，那这一维就没有意义，可以简化为 B-1 维。

比如矩形查询可以被描述为一个 4-Side 的正交范围，但是如果它的下边界必须是 X 轴那么它就是 3-Side 的；而如果左下角必须与原点重合则它是 2-Side 的（也就是二维前缀和）。

扫描线

有时候一个高维的问题难以直接解决，这时候我们就可以考虑把询问离线下来，将其中一维变成时间维，然后用动态的数据结构去维护剩下的维度。

比如下面这个问题：

长为的序列，组询问，每一组给出，求出中在中的数有多少个。，值域。

这相当于是一个二维数点问题。直接做这个是 4-Side 的，比较难；但是我们可以把询问区间这一维作为时间维，这样我们就把问题变成了一维的值域内数个数问题，用树状数组维护即可。时间复杂度。

如图，此时问题变 r 位置的答案减去 l-1 位置的答案。 — 如图，此时问题变位置的答案减去位置的答案。

像这样，利用时间维将静态的 B 维问题降为动态的 B-1 维问题的方法被称为扫描线。

扫描线的基本流程：

对询问按照时间维排序。
维护所有左端点到当前右端点的影响。如果维护信息可差分（如本例）可以不用而是直接在左端点减右端点加。
每次右移右端点时，加入右端点的影响，然后回答所有右端点为当前右端点的询问。

经典问题包括但不限于矩形面积并等。

莫队

Luogu1494 小 Z 的袜子

莫队是一种基于扫描线与分块的离线算法，由著名远古时代集训队选手莫涛发明，可以在根号时间内解决一部分分治数据结构难以解决的区间询问。

适用范围

莫队需要维护子集。如果维护的子集可以插入和删除，那么就可以在的时间复杂度内回答个询问。

基本流程

将询问离线，按照左端点分块，然后按照块排序，块内按右端点升序。

然后维护两个指针，表示这两个指针内的子集的答案，然后通过移动指针向这个子集内增删元素，从一个询问转移到另一个询问。

同阶的情况下，块长为时，时间复杂度最优取得。

时间复杂度证明

设块长为。

对于右端点，由于每个块内部右端点是有序的，所以在每个块内右端点的移动量为，总移动量为。

对于左端点，由于排序后相邻两个左端点的距离不超过（块内不超过），总移动量为。

总时间复杂度。

取得平衡，时间复杂度。

卡常小寄巧

块长开。
奇偶块排序：奇数块内按递增排序，偶数块内按递减排序。

回滚莫队

如果插入和删除中有一个不方便快速操作了怎么办呢？

可以用回滚莫队来解决这个问题，它把操作代价高的那个个改为撤销。

我们下文以不删除的回滚莫队为例。

流程

还是正常分块排序，顺序处理询问。

如果当前询问的右端点块与上一个询问的右端点块不同，则将右端点设为当前块右端点，指针区间设为空。
如果询问的左右端点在同一个块，直接暴力扫描即可。
否则：
- 不断拓展右指针直到抵达这个询问的右端点。
- 不断拓展左指针直到抵达这个询问的左端点。
- 回答询问。
- 撤销左端点的移动，使指针区间变成空。

带修莫队

如果问题带修改，那么需要再加一维时间维，把操作也变成一种转移。

时间复杂度。

线段树分治

LibreOJ121 动态图连通性（不强制在线）

动态加边、删边、查询两点连通性。不强制在线。

线段树分治，顾名思义和线段树脱不了干系。

对于这种“一个操作会影响一个时间区间”的题目，我们对时间维建立一棵线段树，然后把这个时间区间当成线段树的一次修改挂在线段树的结点上。

在挂完所有询问后，我们从线段树的根结点开始依次遍历每个结点。每到一个结点，就把这个节点上挂的所有修改操作都做一遍。

这样到达叶结点时，所有会对当前结点进行影响的修改都已经完成，此时询问得到的就是答案。

注意我们结束对一个结点的访问时需要撤销这个结点上的操作，因此线段树分治常常要用可撤销并查集。

时间复杂度，是区间数。

整体二分

对于那些可以单组询问可以单独二分，但是多组询问且不强制在线的题可以采取整体二分。

整体二分的流程：

设我们现在要求解的询问集合为，并且这些询问的答案都在内。

我们把按照时间维排序，将与这些询问作比较（利用数据结构），将询问分类为“答案不大于 ”和“答案大于 ”两类。

求解“答案不大于 ”的部分，然后用“答案不大于 ”的这部分操作对数据结构进行影响，再去求解“答案大于 ”的部分。

时间复杂度。

总结

在当今任何知识点都不敢裸奔的大时代背景下，数据结构的画风从考察单一算法逐渐变成了思维上多步或者和 DP、图论等一起出现，因此做数据结构题一定要灵活，要着手分析维护物的性质而不是局限于某一个思维定式，否则很容易走到死胡同里。

数据结构大部分都拥有较大的代码量，极易出错，对选手的调试分析能力要求较高，平时做数据结构不能口胡而是一定要自己动手去写去调。