字符串总结

感谢 DeepSeek 对本文写作的大力支持。

字符串

字符串是一串顺序排列的字符。（废话）

以下是一些有关字符串的定义：

字符集：字符串中所有可能出现的字符集合，记为。
下标（index）：位于字符串第个位置的字符下标为（本文采用 1-index）。
子串（substring）：对于任意取出下标范围为的字符依次排列即为一个子串，记为。
子序列（subsequence）：对于任意依次取出排列即为一个子序列。
前缀（prefix）：任意以开头的子串。特别的，当时，称之为真前缀。
后缀（suffix）：任意以结尾的子串。特别的，当时，称之为真后缀。
字典序：对于任意两个字符串，，称字典序小于当且仅当满足以下两个条件之一：
- 存在一个下标，使得，且。
- 。
回文：如果一个字符串等于它的翻转，称它为回文串。

哈希

哈希即映射算法，是整个 OI 界性价比最高的算法几乎没有之一，搭配二分食用后它可以用几乎为零的学习成本和较高的效率解决下文大部分高级算法能解决的问题。

映射

我们知道双射的定义：对于集合，如果存在关系使得中任意一个元素都在中存在且仅存在一个元素与之对应，这个映射就是一个双射。

但是真的要找这样的算法是非常难的，因此我们退一步，如果我们认为这个关系只有极小的概率能让中两个不同元素经过关系后得到相同的结果，那么它就是一个合适的哈希算法。

生活中存在一些这样的哈希算法，比如将快递映射到取件码，将学生映射到学号；也存在一些会发生冲突的哈希算法，比如如果将首字母作为一个人名字的哈希值，就会出现诸如“主席树”之类令人忍俊不禁的情况。

哈希的主要用途是牺牲极小的正确率，将原本需要高时间复杂度比较的元素映射到低时间复杂度比较。这个牺牲的正确率一般是可以计算的：如果将个元素映射到个空间，那么发生冲突的概率为；但是如果将个元素映射到个空间，就有高达的概率发生冲突（生日悖论）。因此选取合适的哈希算法与映射后的空间极为重要。

字符串哈希

字符串哈希是典型的降低比较时间复杂度的算法。

考虑下列问题：

求模式串在文本串中的出现次数。

如果使用朴素算法，就需要对字符串的每个位置都进行一次时间复杂度的匹配，最坏时间复杂度会达到。但是使用字符串哈希，就能将单次匹配的时间复杂度降低为，总时间复杂度。

常用的字符串哈希实际上进行了两次映射：先将字符串映射为（字符集大小）进制数，然后再用取模等方式将其映射到常常为位无符号整数的大小。

关于哈希的具体写法不再赘述。

// 1-indexed
const ll HM[2] = {1000000007, 1000000009};
const ll HB[2] = {911382629, 19260817};
const int M = 1e6 + 5;
// 1-indexed string

ull hb[2][M];

void init_hsh() {
    for (int j = 0; j < 2; ++j) {
        hb[j][0] = 1;
        for (int i = 1; i < M; ++i)
            hb[j][i] = hb[j][i - 1] * HB[j] % HM[j];
    }
}

typedef std::array<ull,2> pul;
template <typename Tp>void cmod(Tp &x,int p){x=(x%p+p)%p;}
struct shsh{
    private:
        vul h[2];
    public:
        shsh(int n,string s):h{vul(n+1),vul(n+1)}{
            for(int j=0;j<2;++j)
                for(int i=1;i<=n;++i)
                    h[j][i]=(h[j][i-1]*HB[j]%HM[j]+s[i])%HM[j];
        }
        pul hsh(int l,int r){
            int len=r-l+1;
            pul x;
            for(int i=0;i<2;++i){
                auto p=h[i][l-1]*hb[i][len]%HM[i];
                cmod(x[i]=h[i][r]+HM[i]-p,HM[i]);
            }
            return x;
        }
};

KMP

（如果你理解不了这一节的内容，直接去看 ACAM 吧）

（本节所有字符串均为 1-indexed）

KMP 算法是一种常用于字符串匹配的算法，以其发明者 Knuth,Morris,Pratt 命名。

Border 与前缀函数

对于字符串，如果它的某个真前缀同时也是它的后缀，则称这个前缀为一个 Border。

对于字符串定义前缀函数表示以结尾的前缀的最长 Border 位置。

对于字符串 abaab，。

求前缀函数

接下来介绍如何快速求前缀函数。

维护当前指针与 Border 指针，表示。初始时。
重复执行以下步骤：
- 。
- 重复执行以下步骤直到：
- - 如果，则。结束本步循环。
- - 如果，结束本步循环。
- - 否则。
求得。

匹配算法流程

求模式串在文本串中的出现次数。

匹配流程与求前缀函数有一些类似之处：

对求出。
接下来维护文本串指针和模式串指针，表示与匹配。初始时。
重复执行以下步骤：
- 。
- 重复执行以下步骤：
- - 如果，则。结束本步循环。
- - 如果，结束本步循环。
- - 否则。
如果在匹配的过程中，说明匹配成功。为继续匹配应当使。

正确性证明

如图。

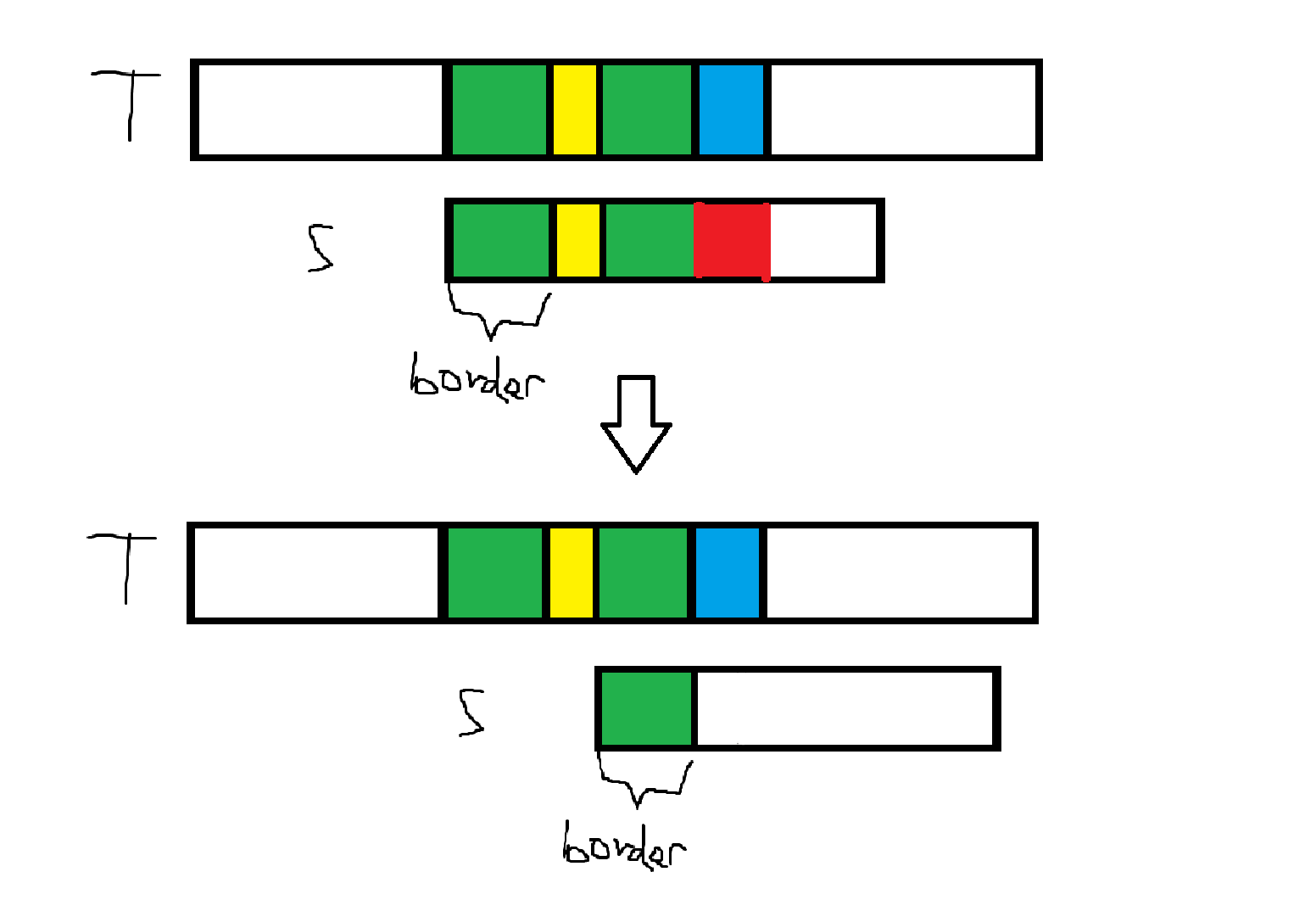
如此我们可以保证指针部分始终匹配。

求等价于的情况，故不再赘述。

时间复杂度证明

由匹配流程可知当自增时至多自增（匹配成功时），因此最多自增次；又因为非负，因此最多减少次，故求时间复杂度。匹配时间复杂度证明类似，为。

模板

struct KMP{
    private:
        vi nxt;
        string s;
        int n;
    public:
        KMP(int _n,string _s):n(_n),s(_s),nxt(_n+1){
            for(int i=2,j=0;i<=n;++i){
                while(j&&s[i]!=s[j+1])j=nxt[j];
                if(s[i]==s[j+1])++j;
                nxt[i]=j;
            }
        }
        vi border(){return nxt;}
        vi match(int m,string t){
            vi ans;
            for(int i=1,j=0;i<=m;++i){
                while(j&&t[i]!=s[j+1])j=nxt[j];
                if(t[i]==s[j+1])++j;
                if(j==n){
                    ans.push_back(i-n+1);
                    j=nxt[j];
                }
            }
            return ans;
        }
};

ACAM

（在阅读以下内容之前，建议先行学习虚树理论，至少理解虚树理论的基本思想）

~~每一个学过算法竞赛的人，都会就这个名字产生无尽的遐想，然后发现这玩意并不能自动 AC~~

AC 自动机（Aho-Corasick AutoMation,ACAM）是一个基于 Trie 树的数据结构（？），可以以时间复杂度解决多模式匹配任务。

AC 自动机在某些意义上与 KMP 有相似之处，但不理解 KMP 也可以先学。

Fail 指针

首先对所有模式串建出 Trie 树。

我们定义某个结点的 fail 指针为去除这个结点对应字符串的前若干个字符后在 Trie 树上存在的最长串。

显然除了根结点（空串）所有结点都一定存在 fail 指针。下图用红色边标注了结点的 fail 指针：

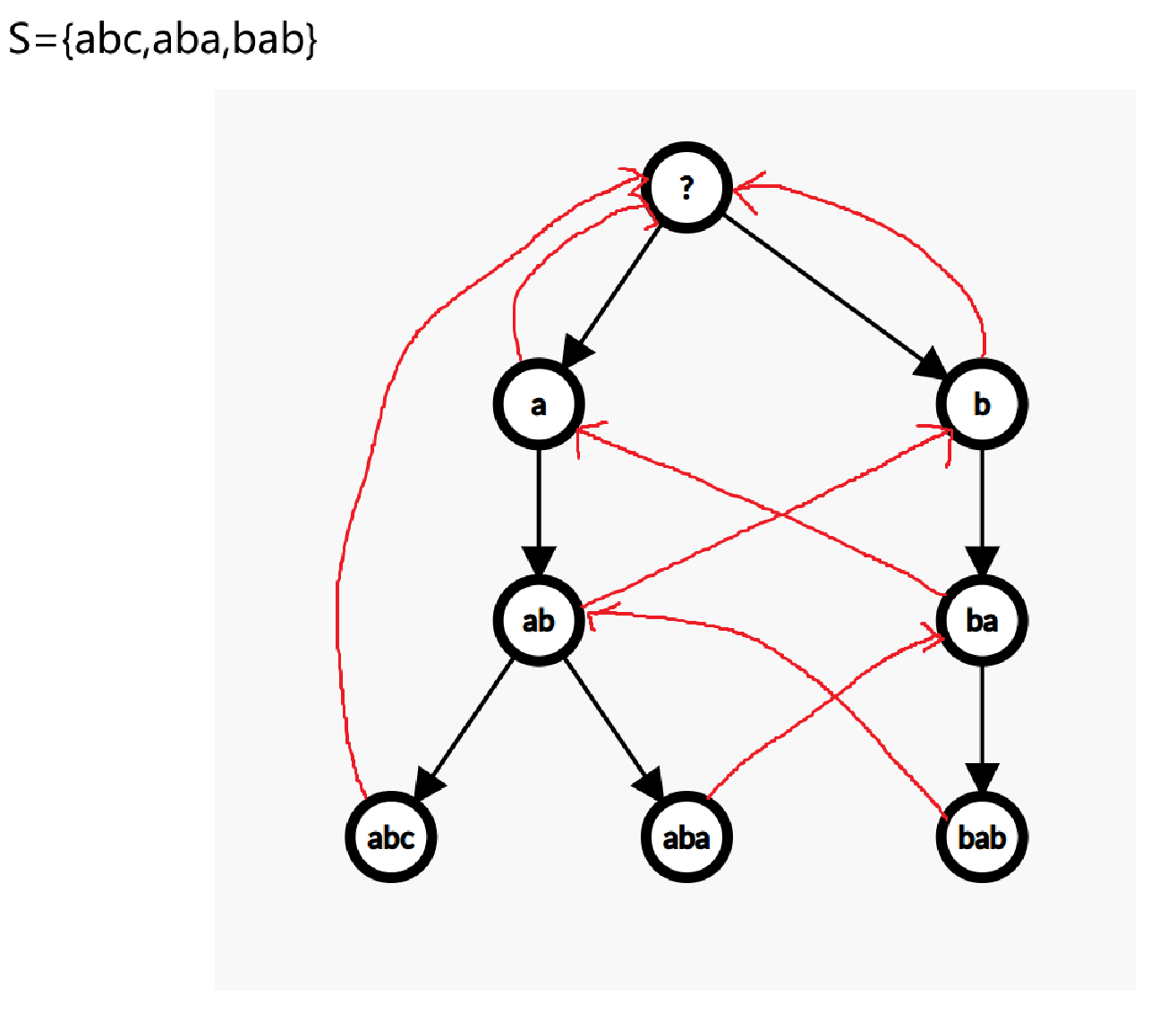
我们可以从其定义发现一些性质：

fail 指针一定是从较长串指向较短串。所以把 fail 指针视为有向边时会发现出现了这些边构成了树结构，任意结点都能不断跳 fail 指针得到空串。这就是 fail 树。
对应到字符串意义上，如果的 fail 指针为，那一定是的后缀。

求 Fail 指针

考虑递归地求 fail 指针。

假设我们已经求得某个结点对应串的 fail 指针为，那么对于其某个儿子，如果存在，那么这个结点就一定是的 fail 指针（显然不存在更长的）；否则跳到的 fail 指针，重复直到找到（或空串）即可。

在完成了 fail 树的构建后，我们就完成了 ACAM 的构建，可以进行匹配了。

算法流程

给定模式串与文本串，求中多少个串在中出现过。

首先我们在 Trie 树中标记所有模式串的结尾位置，然后建 ACAM。

从根节点出发，对于中的每一个字符，不断跳 fail 指针直到存在的转移并转移，并统计其 fail 树上有多少个结尾位置（访问结束后将其标记为已统计）。

容易发现由于任意结点只会在跳 fail 时访问一次（遇到已统计的结点直接退出），所以时间复杂度。

Trie 图

在字符集较小的情况下我们可以通过补齐 Trie 上所有空转移，以的时空复杂度将 ACAM 变为真正的 DFA。但在算法竞赛涉及的领域内的大部分情况下这是个除了省码量以外没用的负优化。

拓扑排序/DFS 优化

Luogu5357 【模板】AC 自动机

给定模式串与文本串，求在中的出现次数。

在这种情况下，我们不能在访问结束后直接将结点标记为已统计优化时间复杂度。由于 fail 树的树高没有保证，最坏情况下时间复杂度将退化为，难以接受。

此时我们注意到每个模式串的出现次数实质上就是其结尾结点在所有跳 fail 树的过程中被访问的次数，也就是子树中被访问到的结尾结点个数。因此我们可以在跑完字符串后对于所有访问过的结点拓扑排序或 DFS 统计子树信息。

最终时间复杂度为。

模板

struct ACAM{
    #define app push_back(0)
    private:
        vector<tnode> T;
        vi fail,end,idx;
        vector<vi> FT;
        int pn;
        int nnode(){
            return T.push_back({}),fail.app,end.app,++pn;
        }
    public:
        ACAM():pn(0),fail(1),end(1),idx(1),T(1){}
        int ch(char x){return x-'a';}
        void ins(string s){
            int p=0;
            for(auto v:s){
                int nx=T[p][ch(v)];
                if(!nx)nx=T[p][ch(v)]=nnode();
                p=nx;
            }
            end[p]++;
            idx.push_back(p);
        }
        void build(){
            std::queue<int> q;
            for(int i=0;i<SIG;++i)if(T[0][i])q.push(T[0][i]);
            while(!q.empty()){
                int p=q.front();q.pop();
                for(int i=0;i<SIG;++i){
                    if(T[p][i]){
                        fail[T[p][i]]=T[fail[p]][i];
                        q.push(T[p][i]);
                    }
                    else T[p][i]=T[fail[p]][i];
                }
            }
        }
        void bft(){
            FT.resize(pn+1);
            for(int i=1;i<=pn;++i)FT[fail[i]].push_back(i);
        }
        void qry(string s){
            vl ans(pn+1);
            int p=0;
            for(auto v:s){
                p=T[p][ch(v)];
                ans[p]++;
            }
            bft();
            function<void(int)> dft=[&](int u){
                for(auto v:FT[u])dft(v),ans[u]+=ans[v];
            };dft(0);
            for(int i=1;i<idx.size();++i)cout<<ans[idx[i]]<<'\n';
        }
    #undef app
};

例题

[POI 2000] 病毒

题意：给定若干个 01 串，是否能构造一个无限长的字符串使得给定的 01 串均不会在这个字符串中出现。

对所有模式串建 ACAM。

考虑字符串匹配的流程，“无限长”等价于存在一种在 AC 自动机上无限匹配而不走到结束结点的方案，容易发现其充要条件为将 AC 自动机视为有向图的情况下存在一个不包含结束结点的环。

[CCF 201509-5] 最佳文章

题意：给定若干模式串，求一个长度为的文本串，最大化文本串中模式串的出现次数。求次数。。

建立 ACAM。定义每个结点对应结束标记个数为。

考虑 DP，表示长度为的文本串，当前结点对应字符串为的最大出现次数。

转移：直接做是的，用广义矩阵乘法快速幂可以优化到。

[BJWC 2011]禁忌

题意：给定模式串集合，求对于所有长度为的字符串以下数值的期望：将任意划分为若干段得到若干子串，所有模式串在这些子串中的总出现次数在所有划分方案中的最大值。。

和上一题一样建立 ACAM，为了方便统计补全 Trie 图。

同样考虑 DP，表示长度为的文本串，当前结点对应字符串为的总出现次数。

转移： $是终止结点：$ 可以注意到和上一题不同的是此题不允许两模式串重叠匹配，所以在遇到终止结点时必须立刻结算答案并跳转回根结点（对应截断前面的部分重新匹配）。

同样矩阵快速幂即可。

[COCI 2015] Divljak

题意：给定模式串集合与初始为空的文本串集合。两种操作：

向中添加一个字符串。

询问在中多少个串中出现过。

对模式串建立 ACAM。

插入时，记在 ACAM 上经过的所有结点序列为，那么“ 在多少个串中出现过”等价于“ fail 树子树中有多少个文本串满足其至少一个出现在其中（很绕，通俗的讲就是 fail 子树中留下了多少个文本串的痕迹）”。

再进一步观察发现，在每次插入时答案会的结点是中所有结点构成的祖先链的并。

容易想到用树状数组维护子树和。但如果直接在这些结点上单点加然后子树求和，在两结点 LCA 以上会算重。

一个常见的 Trick 是，在单点加的同时，在 fail 树 DFN 序相邻的两结点 LCA 处减，可以证明这通操作以后最后所有点都只加了一次。（类似虚树思想）

设总字符数为，最终时间复杂度。

BZOJ4231 回忆树

题意：给定一棵树，每条边上有字符。若干次查询，每次给定一个字符串与两个点，求取出树上到的路径拼接得到的字符串在中出现了多少次。

。

首先考虑匹配串的位置包含 LCA 的情况，容易发现只需取出 LCA 链上长度为且以为中心的部分跑 KMP 即可。

现在只需考虑有祖先关系的两点之间构成的字符串。由于字符串拼接方向并不统一，需要再考虑一遍的反串，并统一规定答案只统计从浅深度向深深度拼接的字符串。

离线询问，对所有的正串与反串建立 ACAM，并对原树进行一次 DFS，过程中同时维护当前拼接得到串的匹配位置。由于答案可以被拆成，接下来就是和上一题差不多的方法，只需要把访问到的 ACAM 结点的 fail 树祖先链全部加一遍（不同的是这题求的是出现总次数不是字符串数，所以不需要那个 Trick），然后统计每个结束结点的字数和，用树状数组即可。

最终时间复杂度。

SA

后缀数组（Suffix Array，SA）是一个可以用于解决大量字符串问题的工具。

后缀排序

对于字符串的所有后缀按照字典序排序的问题被称为后缀排序。为了方便存储，我们使用一个数组来表示排序结果，数组中表示以开头的后缀，这个数组就是后缀数组。

举个例子，对于字符串 abaab，其后缀排序结果为

aab     -> 3
ab      -> 4
abaab   -> 1
b       -> 5
baab    -> 2

所以其 SA 为。

后缀排序有很多种实现方法，这里介绍两种：

Hash+二分

考虑采用传统排序算法框架。

对于两个后缀，如果逐字比较其字典序，单次比较时间复杂度，总时间复杂度。考虑优化。

注意到对于两个后缀，真正需要比较的其实只有 LCP（Longest Common Prefix，最长公共前缀）以后的那一位。如果能快速求 LCP，就能优化时间复杂度。

只需花的时间复杂度预处理哈希，就能以的时间复杂度比较两子串是否相同，这样只需套一层二分就能以的时间复杂度求出 LCP 了。

最终时间复杂度。常数较大。

倍增法

定义表示只考虑每个后缀的至多前个字符得到的排序结果。容易发现时得到的结果即为所求。

显然是易于使用朴素排序算法（或基数排序）快速求得的，接下来的问题在于：能否将的结果拓展到更大的？

答案是肯定的。注意到如果只考虑前个字符的字典序，可以先比较前个字符的字典序，如果前个字符字典序相同再比较后个字符字典序。

我们定义数组表示以开头的后缀的当前排名，那么比较与时只需比较的大小，再比较的大小即可。而数组是易于基于在的时间复杂度内求出的。

此时我们只需执行轮，每轮先对数组基于排序，然后重新计算就能求出。

如果使用快速排序，时间复杂度；如果使用基数排序，时间复杂度。

根据远古时代某 P 氏的实测，如果使用 std::sort 实现快速排序，运行时间约为基数排序的二倍。

除此之外还有一些线性的算法，但是太复杂了不予介绍。

模板

// 1-indexed

vi SA(int n,string s){
    vi sa(n+1),rk(2*n+1),ok;
    for(int i=1;i<=n;++i)sa[i]=i,rk[i]=s[i];
    for(int len=1,p;len<n;len<<=1){
        std::sort(all1(sa),[&](int x,int y){
            return rk[x]==rk[y]?rk[x+len]<rk[y+len]:rk[x]<rk[y];
        });
        p=0;
        ok=rk;
        for(int i=1;i<=n;++i){
            if(ok[sa[i]]!=ok[sa[i-1]]||ok[sa[i]+len]!=ok[sa[i-1]+len])
                ++p;
            rk[sa[i]]=p;
        }
        if(p==n)break;
    }
    return sa;
}

后缀树与 height 数组

（个人认为不理解后缀树是无法理解 height 的含义的，故作介绍）

如果我们想表示一个字符串的所有子串，一个朴素的想法是列举出字符串的所有后缀插入到一棵 Trie 上，上面的任何一个结点都代表一个子串。

然而鉴于这棵树的结点数量为，显式地表示这棵树不现实。

但我们发现由于整棵树只有最多个叶结点，因此一定存在大量的二度点。根据虚树理论，包含全部叶结点的虚树不过个点，并且这棵虚树实质上完整包含了后缀树的拓扑结构（“折叠”了所有二度点），所以只有这些结点值得我们的关注。这棵虚树被称为后缀树。

众所周知建立虚树的方式是对关键点的 DFN 排序，然后相邻 DFN 结点添加 LCA 到虚树中。我们观察在这个场景下 DFN 序等价于所有子串的字典序，又有所有关键点都是叶结点，因此此时添加的 LCA 的字符串本质是字典序相邻的两个后缀的 LCP，而这个结点的高度（深度）即为 LCP 的长度。（根结点深度）

因此我们终于可以心安理得地定义 height 数组：其中表示后缀。

特别的，。

height 数组有以下的性质：

。
- 可以用这个求 height。
。
- 也就是树意义下这个区间内所有关键点的 LCA。

例题

[AHOI2013] 差异

题意：求这个

纯粹的单调栈，极致的享受，丰矿的拆式子，吉列的编码

[SCOI2012] 喵星球上的点名

（老演员。以后还会出现的。）

题意：给定模式串集合与文本串集合，求每个模式串被包含在多少个文本串内，以及每个文本串内出现了多少个模式串。

对于第一问，把所有串都用不同的分隔符串在一起跑 SA。由 height 的性质，对于模式串开头对应的后缀，向左和向右找到的最后一个 height 大于模式串长度的位置构成的区间中的所有文本串对应后缀均合法。

找区间可以用单调栈，而后面的问题本质是区间数颜色种类数，写个莫队就做了。

第二问只需用一个小 Trick：在莫队时如果当前颜色出现次数从到，那么这个颜色的答案直接加上剩余询问数；如果从到则减去剩余询问数。本质是差分。

设总字符数，最终时间复杂度。

（当然可以上 BIT+扫描线做到真）

BZOJ1396 识别子串

题意：给定一个串，对其中每一位求出包含这一位且仅在原串中出现一次的最短子串长度。

求 SA。

“在原串中仅出现一次的子串”对应在 SA 中表现为其长度大于对应后缀的，所以如果绘制出对处能产生的贡献（）的图像大概是一段平直线接上一段斜率为的直线（这段直线实质是直接取的子串）。两部分可以分开用两棵线段树维护。

时间复杂度。

[NOI2016] 优秀的拆分

题意：定义对字符串拆分为四段是“优秀”的，当且仅当这四段满足 AABB 的形式（A,B 均为非空字符串），如将 aabaabaa 拆分成 aab|aab|a|a 是优秀的，a|a|baa|baa 也是优秀的。现在给定一个字符串，求多少种取出子串并将其进行优秀的拆分的方案。

枚举 AA 与 BB 的分界点，现在问题变成如何枚举 AA。

然后一个比较神秘的做法是枚举 A 的长度，然后容易（？？？）发现如果每隔个点设置一个关键点，长度为的 A 就必然会经过其中一个关键点，所以只需要枚举相邻两个关键点分析它们的 LCP 与 LCS（最长公共后缀）长度之和是否大于等于就能判断这两个关键点之间有没有合法的 AA，所以只需要跑 SA 和 "Prefix Array"（反串跑 SA），外层套一个 ST 表就能做了。

由调和级数，这个做法的时间复杂度是。

（闲话：此题的 Hash 做法能获得 95 分，而且导致如果用二分优化甚至能获得满分，令人汗颜）

[HEOI2016/TJOI2016] 字符串

题意：给定字符串，每次询问给，输出的子串中和的 LCP 长度的最大值。

容易发现子串是假的，答案区间一定有。

预处理 SA 后二分答案，问题转化为在区间内寻找满足。由于只需判断真假而不追求答案，可以直接转化为求，转化为 height 就是。由于这个东西在固定的情况下以为中心单峰，只需要对建一棵主席树，每次在区间中找的前驱与后继即可。（另一种思路是对 SA 建主席树，再二分一次找符合条件的上下界，因为说实话求前驱后继并不好写）

如果用 ST 表处理 RMQ，最终时间复杂度。

Manacher

Manacher 是一个用于求解回文子串的算法，优势在于其线性的时间复杂度与非常简单的实现。

朴素算法

求解字符串的所有字串中回文串的个数。

首先为了方便计数，在相邻的字符间添加分隔符，则原字符串的回文子串数是新字符串的奇数长度回文子串数。

对于长度为的的回文串，存在“回文中心”（），使得回文串关于它对称，此时我们称这个为回文半径。那么奇回文子串数就是每个非分隔符位置的回文半径和。

那么我们可以很容易地设计朴素算法，就是每个位置不断向两边拓展其回文半径。这样是的。

优化

考虑能否快速用前个位置的答案算出的答案。

维护包含的最右回文半径位置（最大），设是关于对称的位置，那么一定有。

证明：分情况讨论。

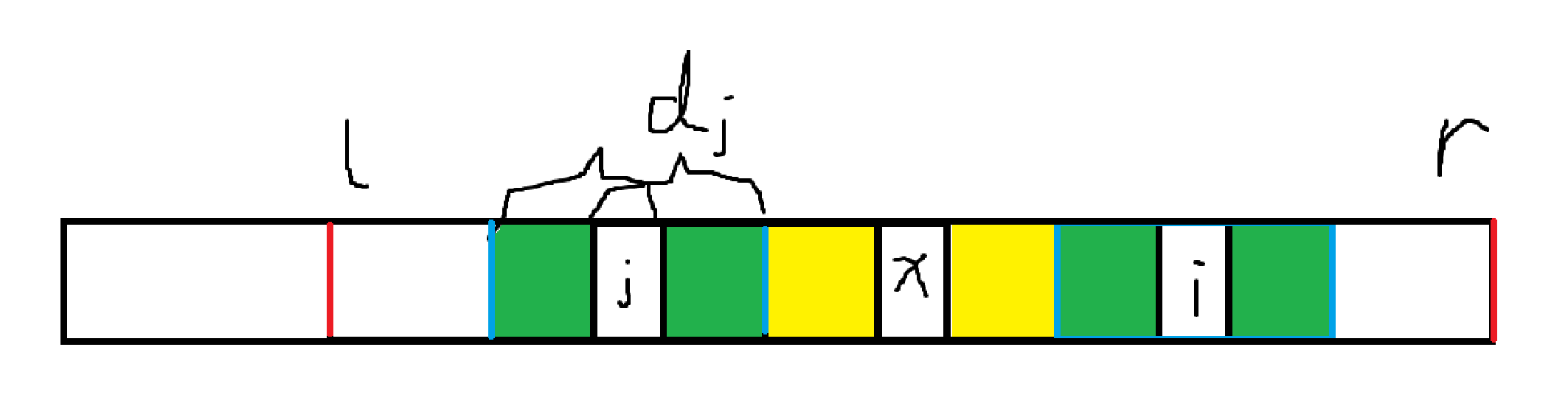
在这种情况下，与以及其周边的情况完全对称，所以。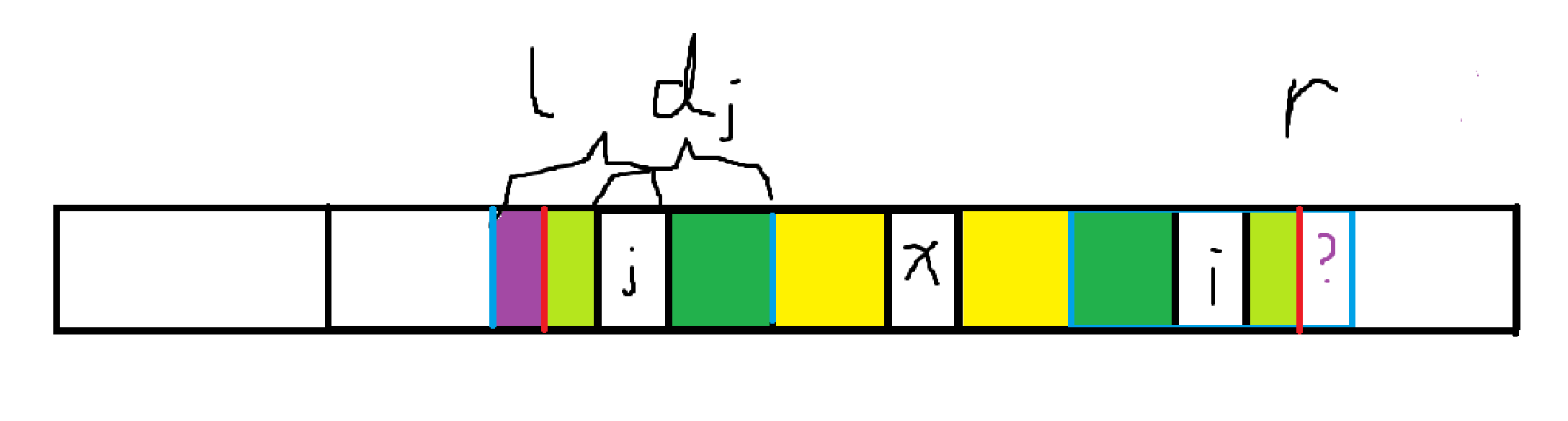
在这种情况下，首先（图示浅绿色部分），而至于图中紫色部分与问号紫色部分是否对称有待验证，进行拓展。

此外还有一种情况，即，在这种情况下我们没有任何可用信息，只能从开始暴力求一次。~~我来成为！~~

至此我们完成了朴素算法的优化。我们发现每次拓展都只增不减，所以最多有次拓展，最终时间复杂度也就是的了。

SAM

后缀自动机（Suffix AutoMaton,SAM）是一个非常强大的数据结构（？），可以在线性时间复杂度下解决大量有关字符串子串的问题。

强烈建议在阅读本段前掌握 ACAM

前置定义

本节包含一些重要的定义，其中包含了 SAM 的精髓，务必熟悉。

为了行文方便，我们做出以下辅助定义：

字符串的长度
：字符串区间构成的子串
字符串集合中，拥有最长长度的字符串
字符串集合中，拥有最短长度的字符串

endpos

对于字符串的任意子串，定义为在中所有出现的位置的末端位置集合。

我知道这段话很绕，所以需要例子辅助理解： ababc，则 ab，因为 ab 在中匹配的位置分别是，因此取这些位置的末端位置构成集合。

特别的，我们认为空串的为全体位置。

我们可以得到下面两条显然的关于的结论（后面会反复用到）：

结论一

如果有子串满足，不妨设，那么一定是的后缀。

结论二

如果有子串，不妨设，那么它们的要么满足，要么满足，当且仅当是后缀时前式成立。

上述两条结论的严格证明比较繁琐，但是结合定义与实例可以轻松理解。

endpos 等价类

我们不妨将所有相同的子串归为一类，称之为等价类（下文简称类）。更为正式的，我们定义等价类表示全体满足的子串构成的集合。

结论三

对于任意类，其中包含的字符串满足：长度为的字符串出现次数均为，且短串是长串的真后缀。

换句话说，给定初始等于，一定存在一种构造方式，每次向的前方添加一个字符直到它等于，使得中的所有字符串都被遍历了一次。

证明：关于后缀的部分由结论二即可得。同时也可以由结论二得到每种长度的字符串只会出现一次。

考虑任意满足它是的后缀，那么显然是它的后缀，那么由结论二可得：。

又由等价类的定义：，因此必须同时取左右两边的等号。证毕。

link 树

由结论二，对于子串，不断地让它向前扩展，它的集合将会越来越小。

形式化地，设的分别为，那么一定满足

我们注意到，中无法取等的位置，对应的意义即为的收缩，而去掉这些无法取等的位置后用等号连接的部分属于同一个等价类，或更强地说，就是一个等价类（结论三）。

此时如果将等价类视为点，这些不等的关系视为边，那么我们可以得到一张图。关于这张图有以下性质：

无环（集合包含的单向性，结论二）
连通（任意点都可以通过不断地缩减到空串以到达全集）

因此，这是一棵树。我们称这棵树为 link 树（或 parent 树）。

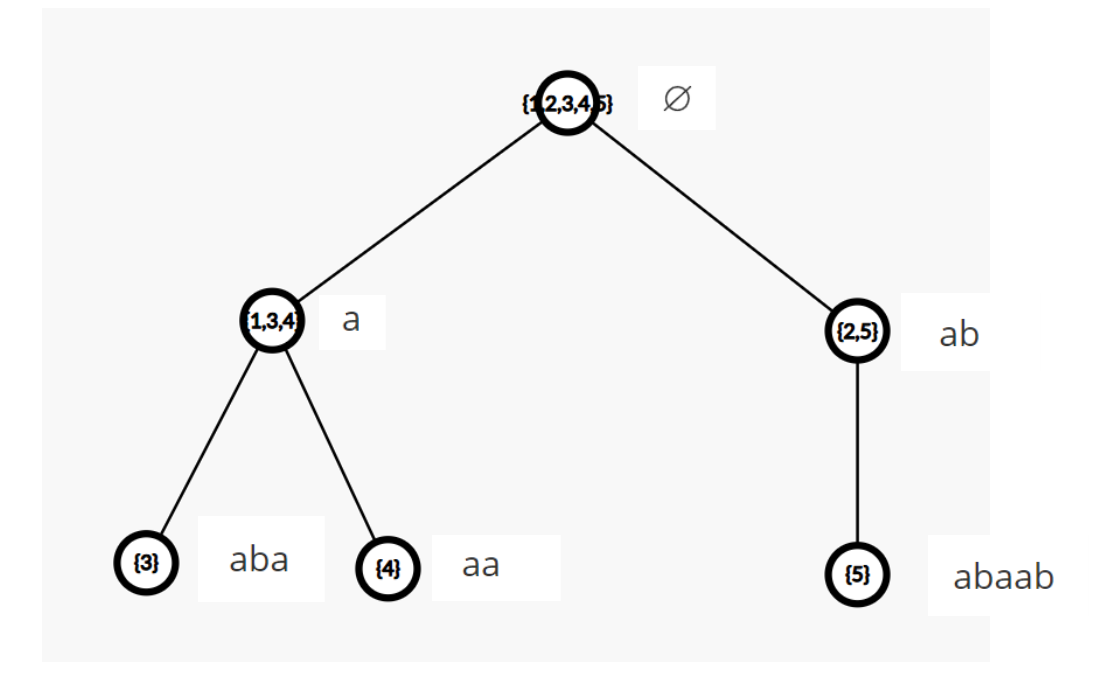
下图是 abaab 的 link 树。为了方便下一步的内容，我们在图中标注每个结点对应类的最长串：

结论四

对于 link 树上的任意结点，均有成立。换句话说，父亲结点对应等价类的最长串长度即为子结点对应等价类的最短串。

结论五

link 树中，每个结点的父亲是该结点的断头指针（即所有等价类中的最长真后缀，类似于 ACAM 和 KMP 的 fail 指针）

引申：link 树中每个结点最长串是所有儿子对应最长串的最长公共后缀。

上文的定义已经验证了这两个结论。

这里需要说明 link 和 fail 的一个区别在于：fail 针对的是一个确切的字符串，而 link 需要首先取出当前等价类中长度最大的后缀，然后对于这个后缀找到其余等价类中最长长度最大的后缀等价类。

SAM 的构建

SAM 是一个 DFA，其中每个结点都代表了一个等价类，每条边都代表一个转移。

SAM 能表示字符串的任意子串，即对于任意子串，从起始结点出发，一定能找到一条路径，该路径表示此子串。

为了实现以上功能，设计了下列算法在线构建 SAM：

流程

定义为上次最后操作的结点，表示类中最长字符串的长度。

初始时，SAM 只有一个结点，。

当插入字符时：

新建结点与转移，
从开始，不断跳父亲结点，沿途添加转移，直到找到结点满足存在转移停下。如果不存在这样的，那么。
- 如果，则。
- 否则执行复制操作。创建一个新结点，从开始向上遍历将沿途所有转移到的转移改为转移到（直到找不到），然后修改。
令。

在插入所有字符后，我们从沿 link 树遍历所有父亲，即为所有终止结点。

正确性证明

FBI Warning：这一节内容极为抽象，也是整篇文章写作过程中耗时最长的部分。如果你是背板选手，请自行跳过这一节。

我知道给谁放上面那个构建方式都头大，所以这一节对于上面的关键步骤都给出详细解释。

首先我们定义一个转移是连续的当且仅当，否则就是不连续的。

新建结点，

~~废话。~~ 好吧还是有用。新建一个结点是因为新字符的加入带来了一个全新的，所以有必要新建一个等价类。

从开始，不断跳父亲结点，沿途添加转移，

回忆 link 树的性质，发现跳 link 树等价于不断切掉前端字符，那么对于树上的这些父亲结点，也理应存在的转移。

直到找到结点满足存在转移停下。

设想一下这种情况：之前的某个后缀已经有了这个转移。对应到字符串上，也就是之前已经添加过了某个子串，满足最后一个字符为，前面的部分是当前的一个后缀。这代表比这个后缀更短的子串都可以通过得到了，故无需再向上跳。

如果不存在这样的，那么。

也就是从来没有过上面提到过的那个子串，那么就不存在什么浪费的问题。忽略即可。

如果，则。

接下来我们记处最长的串为。

当时，一定是中的所有串的前缀，因此存在一个后缀满足它是任意转移到后得到的字符串的前缀（而这个后缀就是），可以直接设置。

否则执行复制操作。创建一个新结点，从开始向上跳树遍历将沿途所有转移到的转移改为转移到（直到找不到），然后修改（直到不存在）。

当时，意味着并非中所有字符串的前缀（有一部分是历经其他连续的路径转移得到的），这时我们就需要从原状态中分离出是后缀的部分，让只留下非前缀的字符串（故），这样就能把链接到上了。这也对应 link 树分裂集合。

我们希望拥有后续所有可能转移到的字符串，因此需要继承的转移；同时上文提到，操作的本质是分裂集合，是子树操作，因此不涉及修改，也应当继承。

同时为了做到彻底的分裂，需要重定向后缀相关的所有到为的转移。这一步只要跳到没有这个转移即可（因为后面不可能有了）。

至于 link 树，我们注意到包含了新的，而只有旧的，对于原有的的串，如果它包含了新的，那么这些新的已经被移走了。为了访问这一部分的后缀，必须将连接到上。

这样，原先的结点不再涉及关于的字符串，相关的字符串全部被移动到了结点上。

时间复杂度分析

谁爱自己研究就研究吧。我累了。

SAM 的性质与应用

紧凑性

SAM 是一个高度压缩的数据结构。可以证明，SAM 的状态数和转移数都为级别。

证明

上述的构建过程已经证明状态数的数量级。初始有个状态，而每次操作最多添加个状态（），故状态数不大于。这一点也可以通过 link 树证明，因为一棵个叶结点的多叉树最多有个结点（二叉树）。

至于转移数，我们首先考虑连续转移数，显然它不可能成无向图意义下的环（否则这两条路径的内容完全一样，完全浪费了），那么这部分不会超过条边（树）；而考察一条从起始状态到任意终止状态非连续转移，一定对应一个非空真后缀，所以非连续转移不超过条。

图论性质

从 SAM 的转移角度看，不难看出它是一个 DAG，且正如前文提到的，对于任意子串，从起始结点出发，一定能找到一条路径，该路径表示此子串。

从 link 树角度看，每个结点表示的字符串数为（结论三）。

模板

其实 SAM 比很多数据结构都短很多的说。。。

实现时如果字符集很小可以空间换时间，否则只能上 umap（并导致时间翻倍）。

// https://www.luogu.com.cn/problem/P3804

const int SIG = 26;

typedef std::array<int,SIG> sam;

//#define pb push_back

struct SAM{
    private:
        vector<sam> G;
        vi len,siz,fa;
        vector<vi> T;
        int pn,lst;
        int nnode(int cl){
            return G.pb({}),len.pb(0),siz.pb(cl^1),fa.pb(0),++pn;
        }
        int ch(char c){return c-'a';}
    public:
        void ins(char _c){
            int cur=nnode(0),p=lst,c=ch(_c);
            len[cur]=len[lst]+1;
            for(;~p&&!G[p][c];p=fa[p])G[p][c]=cur;
            if(~p){
                int q=G[p][c];
                if(len[q]==len[p]+1)fa[cur]=q;
                else{
                    int cl=nnode(1);
                    G[cl]=G[q];len[cl]=len[p]+1;fa[cl]=fa[q];
                    for(;~p&&G[p][c]==q;p=fa[p])G[p][c]=cl;
                    fa[cur]=fa[q]=cl;
                }
            }
            lst=cur;
        }
        void build(){
            T.resize(G.size()+1);
            for(int i=1;i<G.size();++i)T[fa[i]].push_back(i);
            function<void(int)> dfs=[&](int u){
                for(auto v:T[u])dfs(v),siz[u]+=siz[v];
            };dfs(0);
        }
        SAM(string s):pn(0),G(1),len(1),siz(1),fa(1,-1),lst(0){
            for(auto v:s)ins(v);
            build();
        }
        ll qry(){
            ll ans=0;
            function<void(int)> dfs=[&](int u){
                for(auto v:T[u])dfs(v);
                if(siz[u]!=1)cmax(ans,1ll*len[u]*siz[u]);
            };dfs(0);
            return ans;
        }
};

常见应用

求不同子串个数/总长度（[SDOI2016] 生成魔咒）

可以在 DAG 角度 DP，也可以直接用 link 树结论。

求字典序第小子串（[TJOI2015] 弦论）

求出每个结点对应字符串个数后按顺序遍历出边即可。

求 endpos 集合大小

显然可以 dfs link 树，答案为子树大小，但是我们认为只有非复制得到的结点拥有大小（可以认为复制得到的结点在 link 树内直接合并了子树）

查找模式串出现次数

在文本串的 SAM 上跑一遍，如果找到了对应的结点，答案就是这个点 endpos 集合的大小。

求 endpos 集合

如果一定要求确切的 endpos 集合，那就上线段树合并吧。

求两个串的最长公共子串

对其中一个串建立 SAM，把另一个串丢到上面跑同时记录当前长度，失配了就跳 link 树父亲（并同步更新当前长度）。

广义 SAM

主播主播，你的 SAM 固然很强，但还是只能处理单个串，有办法让 SAM 跑在 Trie 上吗？

有的兄弟，有的。

我们发现 Trie 上已经有一些现成的连续转移了，并且对于每个结点，它的也是确定的，所以我们只需要像 ACAM 一样给它暴力跑个广搜，然后照猫画虎地用构建普通 SAM 的方式构建就行了。

例题

[SCOI2012] 喵星球上的点名

题意：给定模式串集合与文本串集合，求每个模式串被包含在多少个文本串内，以及每个文本串内出现了多少个模式串。

对所有文本串加上分隔符建立 SAM，然后把模式串丢到 SAM 上跑，跑到对应结点后第一问的答案就是 link 树子树数颜色，第二问就是到根路径并上有多少个询问点，这两个问题爱咋做咋做，反正是可以做到或者莫队的根号的。（所以这题真不如只上 SA。。。）

[TJOI2019] 甲苯先生和大中锋的字符串

题意：给定字符串，求字符串中出现次数恰好为次的子串中哪个长度出现次数最多，求这个长度（相同长度出现次数时输出最大长度）。

出现次等价于 endpos 集合大小为，求出每个符合条件的 SAM 结点中字符串长度的起止（性质三），做一个差分前缀和就做完了。

[APIO2014] 回文串

题意：定义一个字符串的子串的“存在值”为其出现次数乘以长度，求所有回文子串中“存在值”的最大值。

~~PAM 秒了~~

用 Manacher 求出每个位置的回文半径，标记每个位置回文半径最大值对应的子串终止位置，然后 DFS link 树，这些对应的回文串的出现次数就是其终止位置对应结点对应子树终止状态数。

[ZJOI2015] 诸神眷顾的幻想乡

题意：给你一棵树，每个结点上都有一个字符，求树上的所有点对路径上的字符串依次拼接后能形成多少本质不同的子串。叶结点数很少。

对每个叶结点都为根跑一次 DFS 然后对形成的总 Trie 跑广义 SAM 上就做完了。

[CTSC2012] 熟悉的文章

题意：给定一些模式串和一些文本串。定义文本串的“熟悉度”为，当且仅当存在一种分割文本串的方式，使得其中占总长及以上的子串都满足长度不小于且是某个模式串的子串。对每个文本串最大的。

接下来我们称被划分到模式串子串中的字符是”有用的”。

可以发现答案有单调性，可以二分。考虑怎么 check。

考虑 DP。表示前个字符中最多能有多少个字符有用，容易得到转移直接做是的，但是我们发现如果对模式串建广义 SAM，并预处理出文本串每个位置在广义 SAM 上最长的匹配长度，那么，而单调不减，所以显然这玩意有决策单调性，套一个单调栈就做完了。

最终时间复杂度。

PAM

回文树（Palindromic Tree，又称 EER Tree），又称回文自动机（PAM），是一个可以高效管理字符串的所有回文子串的数据结构（？）。

思想

PAM 与 KMP/ACAM 思想类似，都是用失配指针实现快速跳转。不过我们需要先解决一个问题：如何高效管理长度为奇数和偶数回文串？

答案非常简单：建两棵树不就对了？

所以 PAM 由两棵树构成，每个结点记录其对应串的长度，其两个根分别被称为奇根与偶根，长度分别为与。为了方便匹配，我们认为偶根的失配指针是奇根，而奇根不可能失配。和 Trie 树不太一样的是，沿着树向下走时对应的是在字符串两端都加一个字符。

和 SAM 一样，我们维护上一个字符插入结束后的当前结点 last，在插入新字符时和 ACAM 一样不断跳 fail 指针直到找到结点满足，再在这个结点插入新字符，而这个新结点的 fail 指针就是从开始跳 fail 直到匹配得到的那个结点。

模板

const int SIGMA=26;

typedef std::array<int,SIGMA> pam;

int get(char ch){return ch-'a';}

struct PAM{
    private:
        vector<pam> T;
        vi len,cnt,fi;
        string s;
        int pn,n,lst;
        int nw(int l){
            T.pb(pam());
            fi.pb(0);len.pb(l);cnt.pb(0);
            return ++pn;
        }
        int getf(int p){
            while(s[n-len[p]-1]!=s[n])p=fi[p];
            return p;
        }
    public:
        int ins(char ch){
            s+=ch;++n;
            int p=getf(lst),c=get(ch);
            if(!T[p][c]){
                int q=nw(len[p]+2);
                fi[q]=T[getf(fi[p])][c];
                cnt[q]=cnt[fi[q]]+1;
                T[p][c]=q;
            }
            lst=T[p][c];
            return cnt[lst];
        }
        PAM():s("$"),pn(-1),n(0),lst(0){
            nw(0);nw(-1);
            fi[0]=1;
        }
};